Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
Số phần tử của không gian mẫu 
Gọi A là biến cố: “chọn được 4 đại biểu để trong đó mỗi nước đều có 1 đại biểu và có cả đại biểu
nam và đại biểu nữ”
Số cách chọn 4 người đủ các nước tức là có một nước có 2 người, hai nước còn lại, mỗi nước 1 người là:.
Số cách chọn 4 người đủ các nước và toàn đại biểu nam là:
Số cách chọn 4 người đủ các nước và toàn đại biểu nữ là:
Số phần tử của A là n(A) = 2499- 12 - 550 = 1937
Xác suất của biến cố A: 
Chọn D
Số phần tử của không gian mẫu là: 
.
Gọi A là biến cố “chọn được 4 đại biểu sao cho mỗi Quốc gia đều có ít nhất 1 đại biểu và có cả đại biểu nam và nữ.”
Trường hợp 1: có 2 đại biểu Việt Nam, 1 đại biểu Mỹ, 1 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 1 là: 
cách chọn.
Trường hợp 2: Có 1 đại biểu Việt Nam, 2 đại biểu Mỹ,1 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 2 là:
Trường hợp 3: Có 1 đại biểu Việt Nam, 1 đại biểu Mỹ, 2 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 3 là: 
.
Nên tổng số cách chọn thỏa mãn yêu cầu là: 581 + 678 + 678 = 1937.
Vậy xác suất của biến cố A là: 
.
Không gian mẫu: \(7!\)
Hoán vị 3 đại biểu nam: 3! cách
3 đại biểu nam tạo ra 4 khe trống, xếp 4 đại biểu nữ vào 4 khe trống: \(A_4^4\) cách
Xác suất: \(P=\dfrac{3!.A_4^4}{7!}=...\)
Yêu cầu bài toán tương đương với
\(\frac{\overrightarrow{GA}}{\overrightarrow{GA'}}+\frac{\overrightarrow{GB}}{\overrightarrow{GB'}}+\frac{\overrightarrow{GC}}{\overrightarrow{GC'}}=0\) (1)
Gọi \(X_1\) là điểm trên đường thẳng AB sao cho \(XX_1\) // \(\Delta\) (tức là \(X_1\) là hình chiếu song song của điểm X trên đường thẳng AB theo phương chiếu \(\Delta\) .
Khi đó \(A_1\equiv A,B_1\equiv B,A'_1\equiv B'_1\equiv C'_1,\)
Theo định lí Ta-lét ta có :
\(\frac{\overrightarrow{GA}}{\overrightarrow{GA'}}=\frac{\overrightarrow{G_1A}}{\overrightarrow{G_1A_1'}};\frac{\overrightarrow{GB}}{\overrightarrow{GB'}}=\frac{\overrightarrow{G_1B}}{\overrightarrow{G_1B_1'}};\frac{\overrightarrow{GC}}{\overrightarrow{GC'}}=\frac{\overrightarrow{G_1C_1}}{\overrightarrow{G_1C_1'}};\)
Suy ra
\(\frac{\overrightarrow{GA}}{\overrightarrow{GA'}}+\frac{\overrightarrow{GB}}{\overrightarrow{GB'}}+\frac{\overrightarrow{GC}}{\overrightarrow{GC'}}=\frac{\overrightarrow{G_1A}+\overrightarrow{G_1B}+\overrightarrow{G_1C_1}}{\overrightarrow{G_1A'_1}}=0\)(2)
Lại do \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\) nên \(\overrightarrow{G_1A}+\overrightarrow{G_1B}+\overrightarrow{G_1C_1}=0\)
Vậy \(\overrightarrow{G_1A}+\overrightarrow{G_1B}+\overrightarrow{G_1C_1}=0\)
Từ (1) và (2) suy ra được điều cần chứng minh
a/ Chọn 4 đại biểu từ 4 nước, mỗi nước một đại biểu, có \(4.4.4.4=256\) cách
Còn lại 2 đại biểu chọn bất kì từ 12 đại biểu còn lại: \(C_{12}^2=66\) cách
Vậy có \(256.66=...\) cách
b/
Số cách chọn mỗi đoàn có ko nhiều hơn 2 đb, trong đó 1 đoàn ko có đb nào: \(3.\left(C_4^2\right)^3=...\)
Số cách chọn mỗi đoàn có ko nhiều hơn 2 đb, trong đó đoàn nào cũng có đb: \(4^3\left(C_{12}^2-3.C_4^2\right)=...\)
Số cách chọn thỏa mãn: \(3.\left(C_4^2\right)^3+4^3\left(C_{12}^2-3.C_4^2\right)=...\)
Số cái bắt tay ít nhất đã xảy ra là \(C^2_{20}=20\cdot19:2=190\left(cái\right)\)
a) Cần biết ít nhật ba trong năm đại lượng u1, n, d, un, Sn thì có thể tính được hai đại lượng còn lại.
b) Thực chất đây là năm bài tập nhỏ, mỗi bài ứng với các dữ liệu ở một dòng. Học sinh phải giải từng bài nhỏ rồi mới điền kết quả.
b1) Biết u1 = -2, un = 55, n = 20. Tìm d, Sn
Áp dụng công thức d =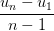 
, Sn =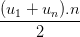 
Đáp số: d = 3, S20 = 530.
b2) Biết d = -4, n = 15, Sn = 120. Tìm u1, un
Áp dụng công thức un = u1 + (n - 1)d và Sn = ,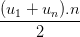
ta có: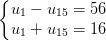 
Giải hệ trên, ta được u1 = 36, u15 = - 20.
Tuy nhiên, nếu sử dụng công thức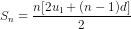 
thì S15 = 120 = 15u1 +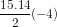 
.
Từ đó ta có u1 = 36 và tìm được u15 = - 20.
b3) Áp dụng công thức un = u1 + (n - 1)d, từ đây ta tìm được n; tiếp theo áp dụng công thức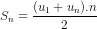 
. Đáp số: n = 28, Sn = 140.
b4) Áp dụng công thức 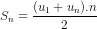, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: u1 = -5, d= 2.
b5) Áp dụng công thức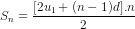 
, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: n = 10, un = -43
Đáp án C
đáp án C