Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |

a) TXĐ: D = [0; + \(\infty\))
\(y'=1+\frac{1}{2\sqrt{x}}\) > 0 với mọi x thuộc D
BBT: x y' y 0 +oo + 0 +oo
Từ BBT => Hàm số đồng biến trên D ;
y đạt cực tiểu bằng 0 tại x = 0
Hàm số không có cực đại
b) TXĐ : D = = [0; + \(\infty\))
\(y'=1-\frac{1}{2\sqrt{x}}\)
\(y'=0\) <=> \(2\sqrt{x}=1\) <=> \(x=\frac{1}{4}\)
x y' y 0 +oo + 0 +oo -1/4 1/4 0 -
Từ BBT: Hàm số đồng biến trên (1/4; + \(\infty\)); nghịch biến trên (0;1/4)
Hàm số đạt cực tiểu = -1/4 tại x = 1/4
Hàm số không có cực đại

Đáp án D
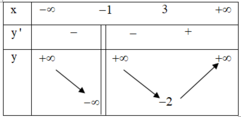
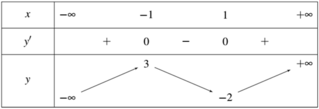
Tại -1 hàm số không xác định nên không nghịch biến trên ( - ∞ ; 3 )

Đáp án D
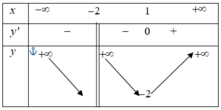
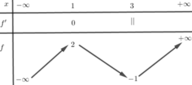
Khẳng định sai là “Hàm số nghịch biến trên khoảng − ∞ ; 1 ” do hàm số không xác định tại x = - 2

Chọn A.
(I) sai f xđ trên R
(II) sai hs có 2 điểm cực trị
(III) ,(IV) đúng

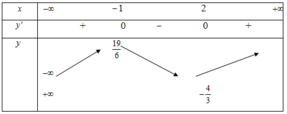
Ta có |f(x)|=10/3→f(x)=10/3 hoặc f(x)= -10/3
Từ bảng biến thiên ta thấy:
Phương trình f(x)=10/3 có 3 nghiệm phân biệt.
Phương trình f(x)= -10/3 có 1 nghiệm
Vậy phương trình đã cho có 4 nghiệm.
Đáp án D

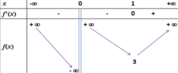
Ta có f(x)-3=0→f(x)=3. Đây là phương trình hoành độ giao điểm giữa đồ thị hàm số y=f(x) và đường thẳng y=3.
Dựa vào bảng biến thiên ta thấy đường thẳng y=3 và đồ thị hàm số y=f(x) có đúng 1 điểm chung.
Đáp án C

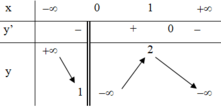
Đáp án D
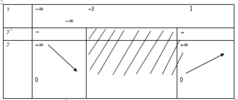
Từ bảng biến thiên ta thấy với m = 2 hoặc m ≤ 1 thì đồ thị hàm số y = f(x) cắt đường thẳng y = m tại 2 điểm phân biệt hay phương trình f(x) = m có 2 nghiệm phân biệt.

Đáp án là D.
• Sai ở bước III (bảng biến thiên)