
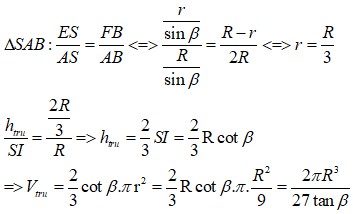
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


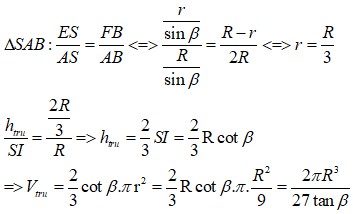

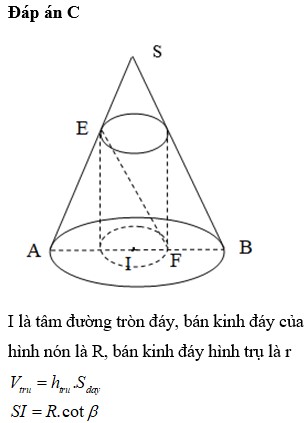
HD: Gọi r, h lần lượt là bán kính đáy, chiều cao của hình trụ
Hình trụ nội tiếp hình nón ![]() (tam giác đồng dạng)
(tam giác đồng dạng)



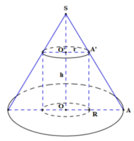
Gọi chiều cao khối trụ là h và bán kính đáy khối trụ là r.
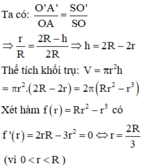
Bảng biến thiên:



Đáp án A.
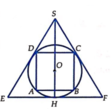
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ S E F đều” (hình vẽ).
Hình vuông ABCD nội tiếp đường tròn (O) nên
A B = B D = 2 R = A B 2 ⇔ A B = 2 R .
⇒ Bán kính đáy và chiều cao của hình trụ (T) lần lượt là r = A B 2 = 2 R 2 và h = A B = 2 R .
Thể tích khối trụ là V T = πr 2 h = π . 2 R 2 2 . 2 R = π 2 R 3 2 .
Ta có ∆ S E F đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của Δ S E F .
Gọi H là trung điểm của EF thì S H = 3 O H = 3 R ⇒ H F = S H . tan 30 ° = R 3
⇒ Bán kính đáy và chiều cao của hình nón (N) lần lượt là H F = R 3 và S H = 3 R . Thể tích khối nón là V N = 1 3 π . HF 2 . SH = 1 3 π R 3 2 . 3 R = 3 πR 3 .
Vậy V T V N = π 2 R 3 2 3 πR 3 = 2 6 .

Đáp án C
Thể tích của khối nón là V n = 1 3 π r 2 h 1 và độ dài đường sinh là l = r 2 + h 2
Thể tích của khối trụ là V t = π r 2 h 2 = 1 3 π r 2 h
Vậy thể tích cái nắp là V = V n + V t = 2 3 π r 2 h
Mặt khác l =1,25
⇒ r 2 + h 2 = 25 4 ⇔ r 2 = 25 4 − h 2
khi đó:
V = 2 3 π h 25 4 − h 2 ≤ 2 π 3 . 125 12 3
Ta có:
V 2 = 4 9 π 2 h 2 25 4 − h 2 2 ≤ 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 ≤ 2 π 2 9 . 25 4 + 25 4 3 3
Dấu bằng xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3
Dấu “=” xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3 ⇒ r = 25 4 − h 2 = 5 6 6 ⇒ r + h ≃ 348 c m