Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

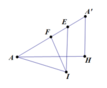
gọi I là tâm đường tròn ngoại tiếp đáy.Do đáy là tam giác đều nên I là trọng tâm
suy ra IA =\( \frac{a\sqrt{3}}{2}\) (giả sử hình lăng trụ là ABC\(A^, B^,C^,\) có cạnh là a)
trong mp(SAI),từ I kẻ đường thẳng d vuông góc vs đáy .Gọi N là trung điểm SA,từ N kẻ đt vuông góc vs SA,cắt d tại O.
O là tâm mặt cầu cần tìm.R=OA=\(\sqrt{OI^2 +AI^2}\)=a
mình xin lỗi chắc tại hôm qua làm muộn đén khuya buồn ngủ quá nên mình làm nhầm.bạn thayS là \(A^,\) cho mình nhé.vậy nên kết quả tìm bán kính sai rồi. nhưng cách làm vẫn tương tự nhé
R=\(\sqrt{0,5^2 a^2 +\frac{a^2}{3}}\) =\(\frac{\sqrt{21}a}{6}\) thông cảm nhé

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C
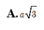
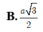
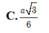
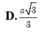

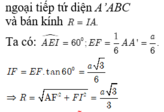
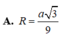
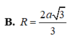
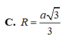
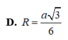

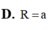

Đáp án C
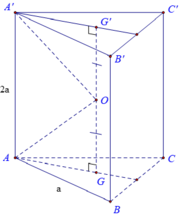
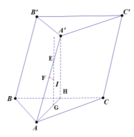
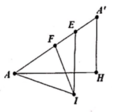
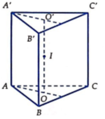
Cho lăng trụ tam giác đều ABC.A'B'C'.
Gọi G, G; lần lượt là tâm của hai đáy ABC và A'B'C'.
Ta có GG' chính là trục của các tam giác ABC và A'B'C' .
Gọi O là trung điểm của GG' thì O cách đều 6 đỉnh của hình lăng trụ
nên là tâm của mặt cầu ngoại tiếp hình lăng trụ. Bán kính mặt cầu là R = OA.
Xét tam giác OAG vuông tại G, ta có: