Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ \(BH\perp CD\left(H\in CD\right)\)
Ta có: ABHD là hình chữ nhật => BH=AD=12 và DH=AB=11
Áp dụng định lí Pytago vào tam giác vuông BHC tại H có: \(HC=\sqrt{BC^2-BH^2}=\sqrt{13^2-12^2}=5\)
=> CD=DH+HC=11+5=16
Áp dụng định lí Pytago vào tam giác vuông ADC tại D có: \(AC=\sqrt{AD^2+CD^2}=\sqrt{12^2+16^2}=20\)
Vậy AC=20cm

Hình:
A B D C H
Giải:
Kẻ BH vuông góc DC
Ta có:
\(\left\{{}\begin{matrix}AB//DH\\\widehat{A}=\widehat{D}=90^0\end{matrix}\right.\)
=> ABHD là hình chữ nhật
\(\Rightarrow DA=AB=11\left(cm\right)\) (1)
Và \(BH=AD=12\left(cm\right)\)
Áp dụng định lý Pitago vào tam giác vuông AHC, có:
\(BH^2+HC^2=BC^2\)
\(\Leftrightarrow HC^2=BC^2-BH^2\)
\(\Leftrightarrow HC=\sqrt{BC^2-BH^2}\)
\(\Leftrightarrow HC=\sqrt{13^2-12^2}\)
\(\Leftrightarrow HC=5\) (2)
Từ (1) và (2) \(\Rightarrow DC=DH+HC=11+5=16\left(cm\right)\)
Áp dụng định lý Pitago vào tam giác vuông ADC, có:
\(AD^2+DC^2=AC^2\)
\(\Leftrightarrow\sqrt{AD^2+DC^2}=AC\)
\(\Leftrightarrow\sqrt{12^2+16^2}=AC\)
\(\Leftrightarrow AC=20\left(cm\right)\)
Vậy ...

Hình thang ABCD có \(\widehat{A}=\widehat{D}=90^o\), AB = 11cm, AD = 12cm, BC = 13cm. Tính độ dài AC

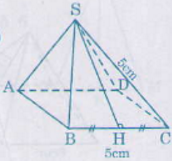



S C 2 = S H 2 + H C 2 = 12 2 + 25 = 169 = 13 2
Vậy SC = 13 cm.
Vậy độ dài cạnh bên là 13cm.
Đáp án cần chọn là: B