Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
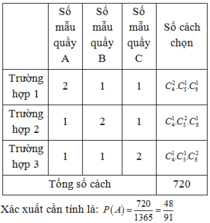
Lấy 4 mẫu thịt lợn trong 15 mẫu có C 15 4 = 1365 cách
Gọi A là biến cô “mẫu thịt của cả 3 mẫu A, B, C đều được chọn”
Khi đó Ω A = C 4 2 . C 5 1 . C 6 1 + C 4 1 . C 5 2 . C 6 1 + C 4 1 . C 5 1 . C 6 2 = 720 cách

Đáp án C.
Điều kiện x > 2 ; x ≠ 4. Phương trình tương đương log 3 x − 2 2 + log 3 x − 4 2 = 0
⇔ log 3 x − 2 2 x − 4 2 = 0 ⇔ x − 2 2 x − 4 2 = 1 ⇔ x = 3.

Chọn A.
Phương pháp:
- Gọi x x ≥ 0 (nghìn đồng) là số tiền tăng lên cho mỗi kg rau.
- Biểu diễn các điều kiện còn lại theo x thu được hàm số ẩn x.
- Tìm GTLN của hàm số trên và kết luận.
Cách giải:
Gọi x x ≥ 0 (nghìn đồng) là số tiền tăng lên cho mỗi kg rau.
Số tiền bán mỗi một kg rau sau khi tăng là x + 30 (nghìn đồng).

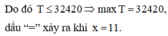
Vậy số tiền nhiều nhất bán được là 32420000 đồng.



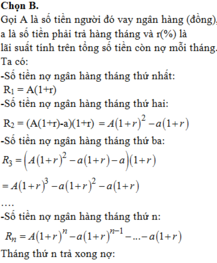

Chọn đáp án A
Gọi a, b lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua đảm bảo lượng protein và lipit trong thức ăn. Theo bài ra ta có số tiền gia đình cần trả là 160a + 110b với a, b thỏa mãn
Do đó, tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì x = a = 0,3; y = b = 1,1