Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng giản đồ vecto
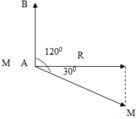
Có: Z C R = 1 3 ⇒ R = 3 Z C ⇒ Z L = 4 Z C
⇒ Z C = 30 Ω = 1 ω C ⇒ C = 1 ω Z C = 1 100 π .30 ⇒ C = 10 − 3 3 π F

Chọn đáp án C
+ Cường độ dòng điện hiệu dụng chạy qua mạch chỉ chứa cuộn cảm thuần: I = U Z L = U 0 2 ωL

Đáp án A
Phương pháp: Cường độ dòng điện hiệu dụng I = U/Z
Đoạn mạch gồm RLC mắc nối tiếp: I = U R 2 + Z L − Z C 2 ( 1 )
Khi nối tắt tụ: I = U R 2 + Z L 2
Từ (1) và (2) ⇒ U R 2 + Z L − Z C 2 = U R 2 + Z L 2 ⇒ Z L − Z C = Z L ( l o a i ) Z L − Z C = − Z L
⇒ 2 Z L = Z C ⇔ 2 ω L = 1 ω C ⇒ ω 2 L C = 0,5

Đáp án A
Phương pháp: Sử dụng hệ thức vuông pha
Cách giải:
Đoạn mạch M chứa R, đoạn MB chứa L và C => u AM và u MB vuông pha với nhau.
=> Ở mọi thời điểm ta có:


Đáp án C
Phương pháp: Mạch điện xoay chiều RLC mắc nối tiếp có L thay đổi
Cách giải:
+ Do u L và u C ngược pha nhau => tại mọi thời điểm ta có:
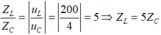
+ Khi L = L 0 thì điện áp hiệu dụng hai đầu cuộn dây đạt cực đại nên:
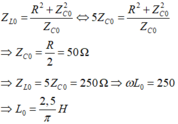
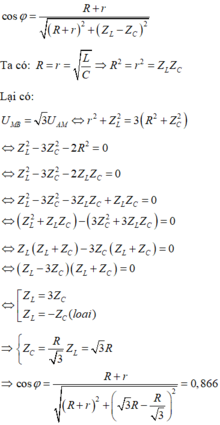
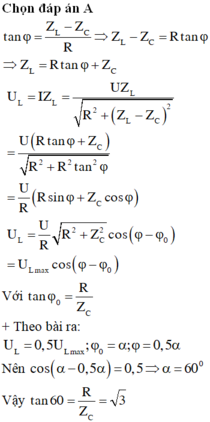
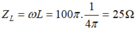
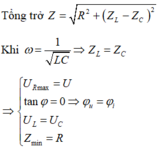
Tổng trở của mạch: \(Z=\frac{U}{I}=\frac{240}{\sqrt{3}}=80\sqrt{3}\left(\Omega\right)\)
\(Z_{MB}=\frac{80\sqrt{3}}{\sqrt{3}}=80\Omega\)
Ta có giản đồ véc tơ theo Z như sau:
i R Z Z Z r Z C AN L MB Z 80 80 80√3 80√2 45° 45° O
Từ giản đồ véc tơ ta có: \(Z_{AN}=80\sqrt{2}\)
Suy ra \(Z_C=80\)
Suy ra tam giác \(ORZ_{AN}\) vuông cân
\(\Rightarrow Z_LZ_{AN}Z_{MB}\) cũng vuông câ
\(\Rightarrow Z_L=80\cos45^0=40\sqrt{2}\)
Từ đó suy ra L
Không thấy hình ạ huhu