
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

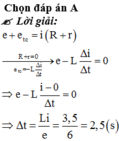

Áp dụng định luật Ôm cho toàn mạch : Tổng các suất điện động trong mạch bằng tổng điện trở toàn mạch nhân với cường độ dòng điện mạch chính.
E + e t c = (R + r)i
Vì R + r = 0 , nên ta có : E - L ∆ i/ ∆ t = 0
Trong khoảng thời gian Δt, cường độ dòng điện i chạy trong cuộn dây dẫntăng dần đều từ giá trị I 0 = 0 đến I = 5,0 A, tức là :
∆ i = I – I 0 = I
Từ đó ta suy ra :
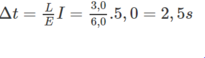

a/ \(\phi=N.BS\cos\left(\overrightarrow{B};\overrightarrow{n}\right)=200.10^{-4}.20.10^{-4}.\cos30^0=2\sqrt{3}.10^{-5}\left(T.m^2\right)\)
b/ \(E_c=\left|\frac{\Delta\phi}{\Delta t}\right|=\left|\frac{-2\sqrt{3}.10^{-5}}{0,01}\right|=2\sqrt{3}.10^{-3}\left(V\right)\)
\(Q=\frac{E_c^2}{R}t=\frac{\left(2\sqrt{3}.10^{-3}\right)^2}{10}.0,01=12.10^{-9}\left(J\right)\)
c/ \(I=\frac{E_c}{R+R'}=\frac{2\sqrt{3}.10^{-3}}{10+2}=\frac{\sqrt{3}.10^{-3}}{6}\left(A\right)\)
Check lại phần tính toán hộ mình nhé, nhiều số quá hơi nhức mắt :(