Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ bảng tần số ta thấy có 8 bao có khối lượng 55kg; 4 bao có khối lượng 60kg và 1 bao có khối lượng 65kg
Nên có 8 + 4 + 1 = 13bao gạo có khối lượng lớn hơn 50kg..
Đáp án cần chọn là: A

Trong kho còn lại:
\(5.6+7+\dfrac{5}{12}-8-\dfrac{5}{8}=\dfrac{527}{120}\left(tấn\right)\)

Tam giác DKE có:
+
+
=900 (tổng ba góc trong của tam giác).
+800 +400=1800
=1800 -1200=
Nên
∆ ABC và ∆KDE có:
AB=KD(gt)
=
=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .
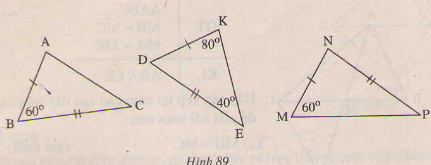
- Tam giác DKE có: ∠D + ∠K + ∠E = 1800 (tổng ba góc trong của tam giác).
hay ∠D + +800 +400 = 1800
⇒∠D = 1800 -1200 = 600
Xét ∆ ABC và ∆KDE có:
AB = KD(gt)
∠B = ∠D ( cùng = 600 )
và BE = ED (gt)
Do đó ∆ABC= ∆KDE (c.g.c)
- Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .

a,Dấu hiệu:Số bao xi măng bán được trong 30 ngày.
Số các giá trị:30
b,Bảng tần số:
|
Bao xi măng(x) |
15 |
20 |
25 |
28 |
30 |
35 |
40 |
|
|
Tần số(n) |
3 |
6 |
4 |
3 |
6 |
5 |
3 |
N=30 |
c,Mình không vẽ được biểu đồ nha”sorry”
d, TB mỗi ngày cửa hàng bán được số bao xi măng là:
X gạch ngang trên X=15.3+20.6+25.4+28.3+30.6+35.5+40.3
Phần 30
=740 phần 30
~24.67
Mốt của dấu hiệu là 20,30,giá trị có tần số là 6
Hay Mo=20,30
a, Dấu hiệu là : số bao xi măng bán được trong 30 ngày
- Số các giá trị là 30
b, Bảng tần số
| Bao xi măng (x) | 15 | 20 | 25 | 28 | 30 | 35 | 40 | |
| Tần số (n) | 3 | 6 | 4 | 3 | 6 | 5 | 3 | N=30 |
c, mình biết vẽ nhưng trên này ko vẽ đc ( sorry)
d, \(\overline{X}\)\(=\frac{15.3+20.6+25.4+28.3+30.6+40.3}{30}=\frac{834}{30}=\frac{412}{15}=27,46\)
\(M_0=30\)
CHÚC BẠN HỌC TỐT![]()

Đăng từng bài một thôi bạn!
1)\(\left(-\dfrac{5}{13}\right)^{2017}.\left(\dfrac{13}{5}\right)^{2016}\)
\(=\left(-\dfrac{5}{13}\right).\left(-\dfrac{5}{13}\right)^{2016}.\left(\dfrac{13}{5}\right)^{2016}\)
\(=\left(-\dfrac{5}{13}\right).\left(\dfrac{5}{13}\right)^{2016}.\left(\dfrac{13}{5}\right)^{2016}\)
\(=\left(-\dfrac{5}{13}\right).\left(\dfrac{5}{13}.\dfrac{13}{5}\right)^{2016}\)
\(=\left(-\dfrac{5}{13}\right).1^{2016}\)
\(=-\dfrac{5}{13}\)

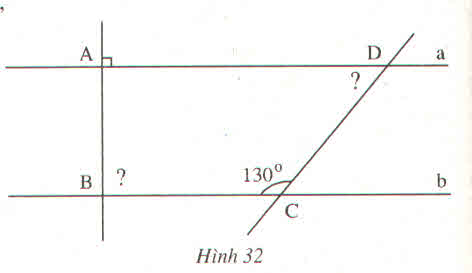
Ta có a // b, nên
góc B = góc A = 90 độ (đồng vị)
Ta lại có \(\widehat{C}+\widehat{D}=180^o\)
hay \(130^o+\widehat{D}=180^o\Rightarrow\widehat{D}=180^o-130^o=50^o\)
vậy góc B = 90 độ
góc C = 50 độ

a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)
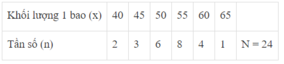


Từ bảng tần số ta có: 8 bao cân nặng 55kg, 4 bao gạo cân nặng 60kg, 1 bao gạo cân nặng 65 kg
Nên có: 8 + 4 + 1 = 13 (bao gạo)
Chọn đáp án A.