Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mỗi thùng có bán kính đáy r chiều cao h(đơn vị mét) thể tích là 
Chi phí làm mỗi thùng bằng 
(triệu đồng). Trước tiên ta cần tìm chi phí nhỏ nhất sản xuất mỗi thùng. Rút 
thay vào
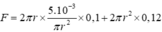
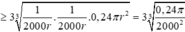
Số thùng tối đa công ty sản xuất được bằng 
thùng.
Chọn đáp án D.
Ta có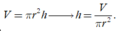 
Gọi t là giá tiền của một đơn vị diện tích vật liệu để làm mặt xung quanh, suy ra giá tiền của một đơn vị diện tích vật liệu để làm mặt đáy là 3t
Diện tích mặt xung quanh 
giá tiền mặt xung quanh là 
Diện tích hai mặt đáy 
giá tiền hai mặt đáy là 
Tổng tiền hoàn thành sản phẩm:
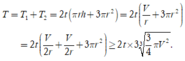
Dấu "=" xảy ra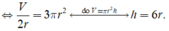 
Chọn C.
Giả sử thùng phi có chiều cao h bán kính đáy r
Diện tích thép tối đa cần dung là:
hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m
Đáp án C
Phương pháp: Lập hàm số chi phí theo một ẩn sau đó tìm giá trị nhỏ nhất của hàm số đó.
Cách giải: Gọi a là chiều dài cạnh đáy hình vuông của hình hộp chữ nhật và b là chiều cao của hình hộp chữ nhật ta có a 2 b = 8 a , b > 0 ⇒ a b = 8 a
Diện tích đáy hình hộp là a 2 và diện tích xung quanh là 4ab nên chi phí để làm thùng tôn là 100 a 2 + 50.4 a b = 100 a 2 + 200 a b = 100 a 2 = 100. 8 a = 100 a 2 + 1600 a = 100 a 2 + 16 a
Áp dụng BĐT Cauchy ta có a 2 + 16 a = a 2 + 8 a + 8 a ≥ 3 a 2 + 8 a + 8 a 3 = 3.4 = 12
Dấu bằng xảy ra khi và chỉ khi a 2 + 8 a ⇔ a = 2.
Vậy chi phí nhỏ nhất bằng 1200000 đồng khi và chỉ khi cạnh đáy hình hộp bằng 2m.
hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra
Đổ 8 lít từ thùng một sang thùng hai thì tổng không thay đổi. Vậy:
Số dầu thùng một là :
( 60 : 3 ) + 8 = 28 ( lít )
Số đầu thùng hai là :
60 - 28 = 32 ( lít )
Đáp số : thùng 1 : 28 lít
thùng 2 :32 lít
gọi x là số lít dầu ở thunhf thứ nhất, y là số lít dầu ở thùng thứ 2 ta có:
x+y=60 => x=60-y
Theo đề bài ta có
2(x-8)=(y+8)
=>2(60-y-8)=y+8
<=> 104-2y=y+8
<=> -2y-y=8-104
<=> -3y =-96
<=> y=32
=> x= 60 -y=60-32=28
Vậy thùng 1 có 28 lít dầu
thùng 2 có 32 lít dầu
Đáp án A
Gọi R và h lần lượt là bán kính và chiều cao của 1 thùng sơn
Suy ra dung tích 1 thùng sơn: V = πR 2 h = 0 , 005 m 3
Gọi n là số thùng sơn tối đa sản xuất được
Tổng chi phí đó bỏ ra là: T = n × 100 . 000 × S x q + 120 . 000 × S d
= n × 100 . 000 × 2 πRh + 120 . 000 × 2 πR 2 ≤ 10 9 ⇔ n ≤ 5 × 10 4 π 10 × Rh + 12 × R 2
Mà 10 R h + 12 R 2 = 5 R h + 5 R h + 12 R 2 ≥ 3 300 R 4 h 2 3 = 3 300 V 2 π 2 3
⇒ n ≤ 5 × 10 4 π 10 × Rh + 12 × R 2 ≤ 5 × 10 4 π 3 × 300 V 2 π 2 3 ≈ 58135 , 9 ⇒ n = 58135 .