Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D.
Gọi xlà khoảng cách từ điểm giữ cốđịnh tới điểm treo cốđịnh, l là chiều dài khi bắt đầu giữ của lòxo. Nên khi này, ta được lò xo mới thực hiện dao động của vật với chiều dài l − x , lấy n = A x
Tại thời điểm giữ lò xo thì thế năng của nó là
W t = W n 2
Khi giữ lò xo, ph'ân thế năng bị mất đi là
W m = x l .W t = x l . W n 2
Ta thấy, khi giữ thì 1 lò xo mới dao động với biên độ k' thỏa mãn
1 − x = kl → k = l − x l
Bảo toàn cơ năng, ta có:
s 2 2 = W − W m ⇒ s 2 2 = kA 2 2 1 − x ln 2
Do đó, ta có A s = A l − x l 1 − x n 2 l với n = A x
Giải ra ta được x l = 5 6

Đáp án D.
Gọi x là khoảng cách từ điểm giữ cố định tới điểm treo cố định, l là chiều dài khi bắt đầu giữ của lò xo. Nên khi này, ta được lò xo mới thực hiện dao động của vật với chiều dài 1-x lấy n = A x
Tại thời điểm giữ lò xo thì thế năng của nó là W t = W n 2
Khi giữ lò xo, phần thế năng bị mất đi là

Ta thấy, khi giữ thì 1 lò xo mới dao động với biên độ k' thỏa mãn
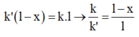
Bảo toàn cơ năng, ta có
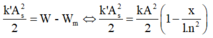
Do đó, ta có
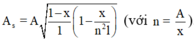
Giải ra được 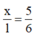

Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5

Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
√3,2 √1,28 √1,92 v O M N
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)


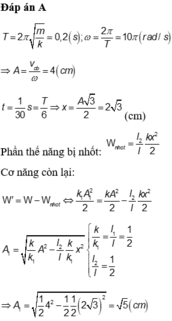
Hướng dẫn:
Tần số góc của dao động ω = k m = 100 0 , 1 = 10 π rad/s → T = 0,2 s.
→ Biên độ dao động của vật A = v m a x ω = 40 π 10 π = 4 cm.
+ Tại t = 0 vật đi qua vị trí cân bằng → sau khoảng thời gian Δ t = T 6 = 1 30 s vật đến vị trí có x = 3 2 A → E d = 0 , 25 E E t = 0 , 75 E
+ Ta giữ cố định điểm chính giữa của lò xo → một nửa thế năng của con lắc bị mất đi theo với nửa lò xo không tham gia vào dao động.
→ Năng lượng của con lắc sau đó E ' = E t 2 + E d = 3 E 8 + E 4 = 5 8 E
+ Lưu ý rằng độ cứng k' của lò xo lúc này k' = 2k → E ' = 5 8 E ↔ 2 k A ' 2 = 5 8 A 2 → A ' = 5 cm.
Đáp án D