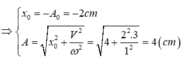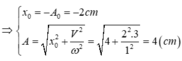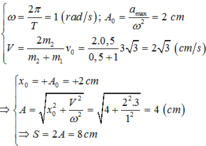Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

Giải thích: Đáp án D
Phương pháp :
- Áp dụng định luật bảo toàn động lượng và định luật bảo toàn động năng
- Sử dung̣ hê ̣thức đôc̣ lâp̣ với thời gian của li đô ̣vàvâṇ tốc
Biên độ dao động ban đầu: ![]()
Cách giải:
Hai vật va chạm đàn hồi xuyên tâm nên áp dụng ĐL bảo toàn động lượng và động năng ta được:
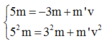
Giải hệ ta được v = 2cm/s
Áp dụng hệ thức độ lập: 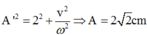
Vậy quãng đường đi được sau va chạm đến khi đổi chiều chuyển động là

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Những bài liên quan đến va chạm đàn hồi đã được giảm tải bạn nhé, chỉ quan tâm đến va chạm mềm thôi.
Bài này phải sửa lại khi lò xo có độ dài cực đại thì gia tốc là 2(cm/s^2)
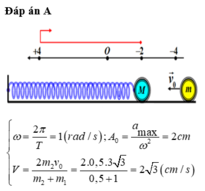
- Khi vật m1 ở vị trí lò xo có độ dài cực đại ---> ở biên --> vận tốc = 0.
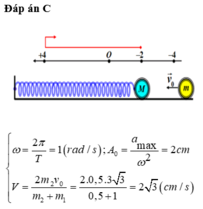
- \(\omega=\frac{2\pi}{T}=1\)(rad/s)
- Biên độ: \(A=\frac{a_{max}}{\omega^2}=\frac{2}{\left(1\right)^2}=2cm\)
- Xét sự va chạm giữa m2 và m1:
+ Bảo toàn động lượng: \(p_t=p_s\Leftrightarrow m_2v=m_1v_1+m_2v_2\Leftrightarrow m_2v=2m_2v_1+m_2v_2\Leftrightarrow v=2v_1+v_2\)(1)
+ Bảo toàn động năng: \(W_{đt}=W_{đs}\Leftrightarrow\frac{1}{2}m_2v^2=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\Leftrightarrow m_2v^2=2m_2v_1^2+m_2v_2^2\Leftrightarrow v^2=2v_1^2+v_2^2\)
\(\Leftrightarrow\left(v-v_2\right)\left(v+v_2\right)=2v_1^2\Leftrightarrow2v_1\left(v+v_2\right)=2v_1^2\Leftrightarrow v+v_2=v_1\)(2)
Từ (1) và (2) suy ra: \(v_1=\frac{2}{3}v=\frac{2}{3}3\sqrt{3}=2\sqrt{3}\)(cm/s)
\(v_2=v_1-v=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\)(cm/s) (dấu - là do vật 2 chuyển động ngược lại)
- Sau va chạm, vật m1 có li độ 2cm, vận tốc: \(2\sqrt{3}cm\)
--> Biên độ dao động mới là: \(A'=\sqrt{x^2+\left(\frac{v}{\omega}\right)^2}=\sqrt{2^2+\left(\frac{2\sqrt{3}}{1}\right)^2}=4cm\)
+ Thời gian kể từ sau va chạm đến khi vật m1 đổi chiều chuyển động (ở biên) là: \(\Delta t=\frac{150}{360}T=\frac{120}{360}.2\pi=\frac{2}{3}\pi\)(s)
+ Quãng đường vật m2 đi được trong thời gian này là: \(S=v.\Delta t=\sqrt{3}.\frac{2}{3}\pi\simeq3,63cm\)
Khoảng cách giữa 2 vật: \(4+2+3,63=9,63\)(cm)
Đáp án C

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B