

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chu kì của dao động T = 2 π m k = 2 π 0 , 2 10 = 0 , 89 s
+ Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 2.10 10 = 2 c m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên là A 1 = X 0 – x 0 = 6 – 2 = 4 c m .
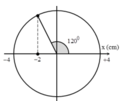
+ Lực đàn hồi của lò xo là nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng, trong nửa chu kì đầu tiên đối vị trí cân bằng tạm O 1 thì vị trí lò xo không biến dạng có li độ x = –2 cm.
→ Thời gian tương ứng Δ t = 120 0 360 0 T = 0 , 296 s
Đáp án A

\(T=2\pi\sqrt{\frac{\Delta l_0}{9}}=0,4s\)
\(\Rightarrow\Delta l_0=4=\frac{A\sqrt{2}}{2}\)
Thời gian lò xo không giãn là \(t=2t-\frac{A\sqrt{2}}{2}\Rightarrow-A=\frac{T}{4}=0,10\left(s\right)\)
Vậy D đúng

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Đáp án D
Biên độ giảm trong khoảng thời gian T 2 là 1 cm
Vị trí cân bằng mới (l) lệch so với vị trí cân bằng cũ là 0,5 cm
Kéo giản thả => đi từ vị trí ban đầu đến 0 là 5 cm, đi một đoạn A 2 = 5 -1 = 4 cm nửa là còn 3 cm => đi vòng lại cái nửa 3 cm thì nó đủ 12 cm lúc này nó nằm tại M . M cách O một đoạn 1 cm, cách I một đoạn 0,5 cm; A 2 đúng là ( 4 – 0,5) cm
⇒ v = ω 3 , 5 2 - 0 , 5 2 = 109 , 5455 c m / s = 1 , 095 m / s

Đáp án D
Trong dao động tắt dần, độ lệch VTCB là Δ l = μ m g k = 0 , 5 ( c m )
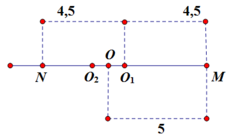
Ban đầu vật ở vị trí M, khi thả vật thì VTCB mới sẽ là O1, biên độ mới A’ = 4,5 cm, vật đi 1 đoạn MN = 9cm. Lúc này vật quay lại VTCB mới O2 với biên độ A ' ’ ’ = 3 , 5 c m .
Theo đề bài, ta phải tìm tốc độ của vật khi vật đi được tổng là 12cm. Lúc này vật đi được 9cm rồi nên cần đi thêm 3cm nữa, tức là tại thời điểm cần tìm tốc độ, vật cách VTCB O2 0,5 cm = > x = 0 , 5 c m . Công thức v = ω A 2 − x 2 = 1 , 095 ( m / s )

Hướng dẫn:
Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 5.0 , 3.10 300 = 0 , 5 c m
+ Biên độ dao động của vật trong nửa chu kì đầu tiên A 1 = X 0 – x 0 = 5 – 0 , 5 = 4 , 5 c m .
+ Biên độ dao động của vật trong nửa chu kì tiếp theo A 2 = A 1 – 2 x 0 = 4 , 5 – 1 = 3 , 5 c m → sau khi đi được quãng đường 12 cm, vật đến vị trí có li độ x2 = –0,5 cm tương ứng với nửa chu kì thứ hai.
→ Tốc độ của vật tại vị trí vật đi được quãng đường S = 12 cm kể từ lúc thả.
v = ω A 2 2 − x 2 2 = 300 0 , 3 3 , 5 2 − 0 , 5 2 = 109 , 54 c m
Đáp án B
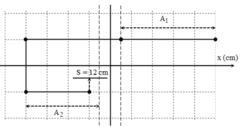
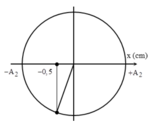

Vị trí cân bằng mới cách VTCB cũ là: \(\frac{\mu mg}{k}=\frac{0,05.0,1.10}{100}=0,05.10^{-2}m=0,05cm\)
Sau nửa chu kỳ biên độ giảm: 2. 0,05 = 0,1cm
Vật đi từ biên phải sang biên trái sẽ đi đc quãng đường là: 5 + 4,9 = 9,9cm.
Như vậy, vật cần đi tiếp: 12 - 9,9 = 2,1 cm
Khi đó, vật cách VTCB mới là: 4,9 - 2,1 - 0,05 = 2,75cm.
Biên độ mới là: A' = 4,9 - 0,05 = 4,85 cm.
Áp dụng CT độc lập, ta có tốc độ của vật là: \(v=\omega\sqrt{A^2-x^2}=10\pi\sqrt{4,85^2-2,75^2}=125,5\)(cm/s)
P/S: Đề bài này hơi lẻ, bạn xem lại giả thiết xem độ cứng lò xo và hệ số ma sát có chính xác như đề bài cho không?

Hướng dẫn:
+ Độ biến dạng của lò xo tại vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 1.10 100 = 10 − 3 m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên A 1 = X 0 – x 0 .
Cứ sau mỗi nửa chu kì, kể từ nửa chu kì thứ 2 biên độ của vật dao động so với các vị trí cân bằng tạm sẽ giảm 2 x 0 .
→ Ta xét tỉ số A 1 2 x 0 = X 0 − x 0 2 x 0 = 0 , 1 − 10 − 3 2.10 − 3 = 49 , 5
→ Biên độ của vật sau 49 nửa chu kì tiếp theo là A 49 = A 1 – ( 49 . 2 + 1 ) x 0 = 1 m m → vật tắt dần tại đúng vị trí lò xo không biến dạng.
+ Áp dụng định luật bảo toàn và chuyển hóa năng lượng ta có 1 2 k X 0 2 = μ m g S → S = k X 0 2 2 μ m g = 100.0 , 1 2 2.0 , 1.0 , 1.10 = 5 m
Đáp án B