Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

từ công thức \(T=2\pi\sqrt{\frac{l}{g}}\) suy ra \(T^2\) tỷ lệ thuận với \(l\)
Ta có \(\frac{l}{l-16}=\frac{T^2_1}{T^2_2}=\frac{\left(\frac{\Delta t}{6}\right)^2}{\left(\frac{\Delta t}{10}\right)^2}=\frac{25}{9}=\frac{25}{25-16}\)
Vậy l=25cm

Đáp án B
Phương pháp: Áp dụng công thức tính chu kì con lắc đơn: T = 2 π l g
Chu kì T là thời gian vật thực hiện một dao động toàn phần
Cách giải:
+ Khi chiều dài của con lắc đơn là l thì: T = 2 π l g = ∆ t 6 ( 1 )
+ Khi chiều dài của con lắc giảm đi 16 cmm thì: T' = T = 2 π l - 16 g = ∆ t 10 ( 2 )
Từ (1) và (2) ta có:
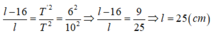
Chọn B

Phương pháp:Chu kì dao động là thời gian vật thực hiện hết một dao động toàn phần
Công thức: T = ∆ t N = 2 π l g (N là số dao động toàn phần thực hiện trong thời gian ∆t)
Cách giải:
Ta có:
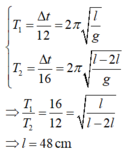
Đáp án C

Tần số dao động cỉa con lắc đơn là:
\(f=\frac{n}{T}\Leftrightarrow f=\frac{500}{100}=5\left(Hz\right)\)
=> B đúng

\(T=2\pi\sqrt{\frac{l}{g}}\)
\(T'=2\pi\sqrt{\frac{l'}{g}}\)
\(\Rightarrow\frac{T'}{T}=\sqrt{\frac{l'}{l}}=\sqrt{2}\Rightarrow T'=2\sqrt{2}s\)
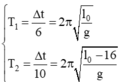
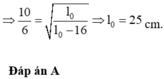
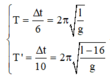
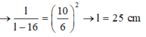
Chọn B
+ Ta có: Δt = 6T1 = 10T2 → 6 . 2 π l g = 10 . 2 π l - 0 , 16 g
+ Giải phương trình ta được: l = 25cm.