Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
+ Chiếc xe xóc mạnh nhất khi chu kì xóc (bị cưỡng bức do đi qua các rãnh) đúng bằng chu kì dao động riêng của xe t = S v = 2 s → v = 10 m/s.
Đáp án B

Chọn B
+ Độ cứng của hệ hai lò xo bằng tổng 2 độ cứng: khệ = 2k = 400 (N/m).
+ v = 14,4 km/h = 4 m/s
+ Xe rung mạnh khi chu kỳ dao động riêng của vật trùng chu kỳ gặp rãnh:
2 π m k h = S v ⇔ 2 π m 400 = 6 4 = 1 , 5 ⇒ m = 22 , 5 kg .

Đáp án B
Phương pháp: Áp dụng điều kiện có cộng hưởng trong dao động cưỡng bức
Cách giải: Để nước trong thùng sánh mạnh nhất thì vận tốc người đó phải đi là
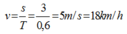

C không đúng vì để làm được như vậy thì cần qua một cơ cấu hệ phức tạp chứ không phải là đơn giản.
Đơn giản nhất theo mình nghĩ là tác dụng lên hệ một dao động tuần hoàn theo thời gian (là dao động cưỡng bức)
@Nguyễn Quang Hưng: bạn ơi nếu đáp án D mình tưởng xe giảm xóc càng lâu càng tốt chứ. để giúp êm xe mà.
như vậy có lợi sao cần phải tắt dần nhanh

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Đáp án A
Phương pháp: Sử dụng lí thuyết về điều kiện xảy ra cộng hưởng của dao động cưỡng bức
Cách giải:
Để xe xóc mạnh nhất tức là xảy ra cộng hưởng chu kì của ngoại lực bằng chu kì dao động riêng của khung xe thời gian đi giữa hai rãnh nhỏ liên tiếp là 1,5s.
Khi đó: 15 v = 1 , 5 s ⇒ v = 10 m / s = 36 km/h