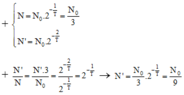Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ban đầu có \(N_0\) hạt
Sau 1 năm, còn lại \(N_1=\dfrac{N_0}{3}\)
Sau 1 năm nữa, còn lại là: \(N_2=\dfrac{N_1}{3}=\dfrac{N_0}{9}\)
Chọn C.
Ban đầu có N0N0 hạt
Sau 1 năm, còn lại N1=N03N1=N03
Sau 1 năm nữa, còn lại là: N2=N13=N09N2=N13=N09
Chọn C.

Chọn đáp án A.
Tỉ số giữa số hạt còn lại và số hạt ban đầu sau 1 năm:
N N 0 = 1 3 ⇔ 2 − t T = 1 3
Tỉ số giữa số hạt còn lại và số hạt ban đầu sau 2 năm:
N ' N 0 = 2 − 2 T = 2 − 1 T 2 = 1 3 2 = 1 9 .
Từ đó suy ra số hạt nhân đã bị phân rã sau 2 năm là:
Δ N ' = N 0 − N ' = 8 N 0 9 .

Đáp án B
Tỉ số giữa số hạt còn lại và số hạt ban đầu sau 1 năm:
N N 0 = 1 3 ⇔ 2 - t T = 1 3
Tỉ số giữa số hạt còn lại và số hạt ban đầu sau 2 năm:
N ' N 0 = 2 - 2 T = ( 1 3 ) 2 = 1 9
Từ đó suy ra số hạt nhân đã bị phân rã sau 2 năm là:
∆ N ' = N 0 - N ' = 8 N 0 9

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)

Sau thời gian t1 số hạt nhân còn lại là
\(N = N_0 2^{-\frac{t}{T}}\)=> \(\frac{N}{N_0}= 0,2= 2^{-\frac{t_1}{T}}=> t_1 = -T.\ln_20,2.\)
Sau thời điểm t2 thì số hạt nhân còn lại là
\(N_1 = N_0 2^{-\frac{t_2}{T}}=> \frac{N}{N_0} = 0,05 = 2^{-\frac{t_2}{T}}\)=> \(t_2 = -T\ln_20,05.\)
Mà \(t_2 = t_1 +100\)
=> \(-T \ln_2 0,05 = -T\ln_2 0,2 + 100\)
=> \(T = \frac{100}{\ln_2{(0,2/0,05)}}=50 s. \)

Số hạt X còn lại là: \(N=\dfrac{N_0}{2^{\dfrac{t}{T}}}=\dfrac{N_0}{8}\)
Số hạt X bị phân rã: \(\Delta N=N_0-N=\dfrac{7}{8}N_0\)