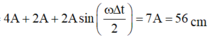Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

> O x M 7 -7 π/3
Quỹ đạo chuyển động là 14 cm → A = 7 cm.
Tại thời điểm ${t_0}$ chất điểm ở vị trí M có pha ban đầu là –π/3; độ lớn gia tốc cực đại tại biên.
→ từ M đến biên lần thứ 3 thì ∆φ = π/3 + 2π = 7π/3 rad.
→ t = ∆φ/ω = 7/6 s và s = 3,5 + 28 = 31,5 cm
→ v = s/t = 27 cm/s.

Đáp án A
Ta có: Δ t = 0 , 1 = 1 3 T
Quãng đường lớn nhất và nhỏ nhất vật đi được trong thời gian Δ t = 0 , 1 = 1 3 T
S min T 3 = 2 A − A 2 = A = 5 c m S max T 3 = 2. A 3 2 = A 2 = 5 3 ⇒ 5 c m ≤ s ≤ 5 3 c m
Vậy trong khoảng thời gian 0,1 s chất điểm không thể đi được quãng đường 9 cm

Đáp án A
+ Quãng đường lớn nhất và nhỏ nhất mà vật có thể đi được trong khoảng thời gian một phần ba chu kì:


ü Đáp án D
+ Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ + 4 cm đến vị trí có li độ -4 cm là Δ t = T 6 ⇒ T = 0 , 6 s
Quãng đường lớn nhất vật đi được trong 1 s là:
S m a x = S T + S T 2 + S Δ t = 0 , 1 = 4 A + 2 A + 2 A sin ω Δ t 2 = 7 A = 56 c m

Đáp án D
Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ +4 cm đến vị trí có li độ - 4cm là
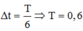 s
s
Quãng đường lớn nhất vật đi được trong 1s là:
![]()
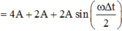
= 7a = 56cm

Ta thấy trên nửa đường thẳng thẳng kẻ từ A và vuông góc với AB có 4 điểm theo thứ tự M, N, P, Q dao động với biên độ cực đại, nên trên AB có 9 điểm dao động với biên độ cực đai với - 4 ≤ k ≤ 4 ( d2 – d1 = kλ)
A B x M N P Q
Cực đại tại M, N, P, Q ứng với k = 1; 2; 3; 4
Đặt AB = a
Tại C trên Ax là điểm dao động với biên độ cực đại:
CB – CA = kλ (*)
CB2 – CA2 = a2 → (CB + CA) (CB – CA) = a2
CB + CA = \(\dfrac{a^2}{k.\lambda}\)(**)
Từ (*) và (**) suy ra \(CA=\dfrac{a^2}{2k.\lambda}-\dfrac{k}{2}\lambda\)
Tại M: ứng với k = 1: MA = \(\dfrac{a^2}{2\lambda}\)- 0,5λ (1)
Tại N: ứng với k = 2: NA = \(\dfrac{a^2}{4\lambda}\)- λ (2)
Tại P: ứng với k = 3: PA = \(\dfrac{a^2}{6\lambda}\) - 1,5 λ (3)
Tại Q: ứng với k = 4: QA = \(\dfrac{a^2}{8\lambda}\) - 2 λ (4)
Lấy (1) – (2) : MN = MA – NA = \(\dfrac{a^2}{4\lambda}\) + 0,5λ = 22,25 cm (5)
Lấy (2) – (3) : NP = NA – PA = \(\dfrac{a^2}{12\lambda}\) + 0,5λ = 8,75 cm (6)
Lấy (5) - (6) → \(\dfrac{a^2}{\lambda}\) = 81 (cm) và λ = 4 cm .
Thế vào (4) → QA = 2,125 cm.
thầy có thể giải thích e chổ CB-CA= Klamda . Với tại s CB= K/2 lamda k thầy?