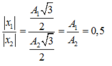Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Hướng dẫn:
Ta có thể quy bài toán con lắc lò xo trong thang máy chuyển động với gia tốc về trường hợp con lắc chịu tác dụng của trường lực ngoài F → = F q t → = − m a → .
Để đơn giản, ta có thể chia chuyển động của con lắc thành hai giai đoạn:
Giai đoạn 1: Thang máy chuyển động nhanh dần đều đi lên, con lắc dao động điều hòa quanh vị trí cân bằng mới O′.
Dưới tác dụng của lực quán tính ngược chiều với gia tốc, vị trí cân bằng mới O′ của con lắc nằm phía dưới vị trí cân bằng cũ O một đoạn O O ' = m a k = 0 , 4.4 100 = 1 , 6 cm.
+ Biến cố xảy ra không làm thay đổi tần số góc của dao động ω = k m = 100 0 , 4 = 5 π rad/s → T = 0,4 s.
Thời điểm thang máy bắt đầu chuyển động, vật ở biên trên, do vậy sau khoảng thời gian Δt = 12,5T = 5 s vật sẽ đến vị trí biên dưới, cách vị trí cân bằng cũ O một đoạn 2OO′ = 3,2 cm.
Giai đoạn 2: Thang máy chuyển động thẳng đều, con lắc dao động điều hòa quanh vị trí cân bằng O.
+ Thang máy chuyển động thẳng đều → a = 0, không còn lực quán tính nữa vị trí cân bằng bây giờ trở về O.
→ Con lắc sẽ dao đông với biên độ mới A′ = 2OO′ = 3,2 cm.
→ Thế năng đàn hồi của con lắc cực đại khi con lắc ở biên dưới, tại vị trí này lò xo giãn Δ l m a x = A ' + m g k = 3 , 2 + 0 , 4.10 100 = 7 , 2 cm.
+ Thế năng đàn hồi cực đại E d h m a x = 1 2 k Δ l m a x 2 = 1 2 .100 0 , 072 2 ≈ 0 , 26 J.

Khi thang máy đi lên lực căng của dây cáp treo thang máy là:
T=(m1+m2)(g+a)(1)T=(m1+m2)(g+a)(1)
và lực ép của người lên mặt sàn thang máy có độ lớn:
N=m2(g+a)N=m2(g+a)
a) Trường hợp thang máy đi lên. Chọn chiều dương là chiều chuyển động. Dựa vào đồ thị ta nhận thấy:
- Ứng với đoạn OA trên đồ thị, thang máy chuyển động nhanh dần đều với gia tốc
a1=52=2,5m/s2a1=52=2,5m/s2
Theo (1)(1) lực căng của dây cáp bằng:
T1=(m1+m2)(g+a1)=6250NT1=(m1+m2)(g+a1)=6250N
Theo (2)(2) lực ép của người lên mặt sàn thang máy bằng:
N1=m2(g+a)=625NN1=m2(g+a)=625N
- Ứng với đoạn AB thăng máy chuyển động thẳng đều (a=0)(a=0) lực căng của dây cáp là: T2=(m1+m2)g=5000NT2=(m1+m2)g=5000N
và lực éo của người lên mặt sàn thang máy bằng:
N2=m2g=500NN2=m2g=500N
- Ứng với đoạn BC trên đồ thị, thang máy chuyển động chậm dần đều với gia tốc
a2=−52=−2,5m/s2a2=−52=−2,5m/s2
Lực căng của dây cáp là: T3=(m1+m2)(g+a2)=3750NT3=(m1+m2)(g+a2)=3750N
Lực ép của người lên mặt sàn là: N3=m2(g+a)=375NN3=m2(g+a)=375N
b) Trường hợp thang máy đi xuống dưới
Chọn chiều dương hướng xuống dưới.
- Ứng với đoạn OA trên đồ thị, thang máy chuyển động nhanh dần đều với gia tốc a′1=2,5m/s2a1′=2,5m/s2. Lực căng của dây cáp là
T′1=(m1+m2)(g−a′1)=3750N=T3T1′=(m1+m2)(g−a1′)=3750N=T3
Lực ép của người lên mặt sàn thang máy là:
N′1=m1(g−a′1)=375N=N3N1′=m1(g−a1′)=375N=N3
- Ứng với đoạn AB của đồ thị, thang máy chuyển động thẳng đều, lực căng của dây cáp bằng:
T′2=(m1+m2)g=5000N=T2T2′=(m1+m2)g=5000N=T2
Lực ép của người lên mặt sàn thang máy là:
N′2=m2g=500N=N2N2′=m2g=500N=N2
- Ứng với đoạn Bc trên đồ thị, thang máy chuyển động chậm dần đều với gia tốc a′2=−2,5m/s2a2′=−2,5m/s2. Lực căng của dây cáp là:
T′3=(m1+m2)(g−a′2)=6250N=T1T3′=(m1+m2)(g−a2′)=6250N=T1
Lực ép của người lên mặt sàn thang máy là:
N′3=m2(g−a′2)=625N=N1N3′=m2(g−a2′)=625N=N1
c) Quãng đường thang máy đã đi lên có thể bằng diện tích của hình thang OABC, và bằng s=(AB+OC)2.AH=60ms=(AB+OC)2.AH=60m. Vận tốc trung bình của thang máy trong suốt thời gian đi lên bằng:
v⃗ =st=6014≈4,29m/sv→=st=6014≈4,29m/s
Mk nghĩ z

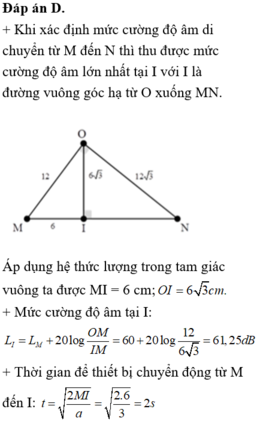
Hướng dẫn: Chọn đáp án D
![]()
![]()
Vì số liệu ở các phương án lệch xa nhau nên ta có thể giải nhanh theo cách 2 (xem x C ≈ 0 )
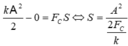
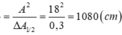
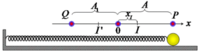
Chú ý: Giả sử lúc đầu vật ở P, để tính tốc độ tại O thì có thể làm theo các cách sau:
Cách 1: Độ giảm cơ năng đúng bằng công của lực ma sát:
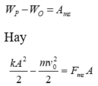


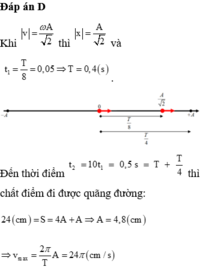
Đáp án C
- Tại thời điểm t = 0 hai điểm sáng cùng đi qua VTCB theo chiều dương
+ Phương trình dao động của hai điểm sáng:

+ Ở VTCB theo chiều dương hai điểm sáng có cùng độ lớn vật tốc

- Công thức tính vận tốc tại thời điểm t: ![]()
Khi vận tốc của điểm sáng 1 bằng 0 thì vận tốc của điểm sáng 2 mới giảm lần:
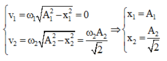
Biểu diễn trên đường tròn lượng giác ta có:
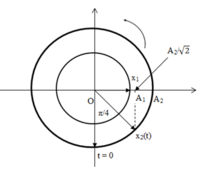
Từ đường tròn lượng giác ta thấy: cùng trong khoảng thời gian t, góc quét được của hai chất điểm lần lượt là:
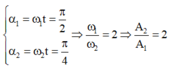
- Thời điểm hai điểm sáng có cùng vận tốc:
![]()
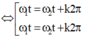
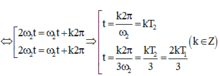
Với k = 0 => thời điểm đầu tiên hai điểm sáng có cùng độ lớn vận tốc.
Với k = 1 => thời điểm tiếp theo hai điểm sáng có cùng độ lớn vận tốc là: ![]()
=> Góc quét được tương ứng của hai chất điểm trên đường tròn:

Biểu diễn trên đường tròn lượng giác:
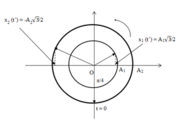
Từ đường tròn lượng giác ta có tỉ số độ lớn li độ của hai điểm sáng: