Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
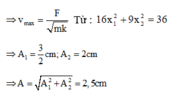
Lực kéo về cực đại tác dụng lên chất điểm trong quá trình dao động là :
F k v m a x = k A = m ω 2 A = 0 , 3 . 10 2 . 0 , 025 = 0 , 75 N

Đáp án B
Phương pháp : Sử dụng công thức tính biên đô ̣của dao động tổng hợp
Lực hồi phục cực đại: Fmax = mω2A
Cách giải :
Từ giả thuyết:
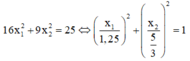
Hai dao động này vuông pha với các biên độ thành phần A1 = 0,8cm, A2 = 0,6cm
Biên độ dao động tổng hợp:
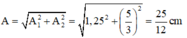
Mặt khác:
![]()
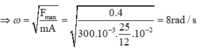

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Bài 2:
\(T=2s\Rightarrow\omega=\frac{2\pi}{T}=\pi\left(rad/s\right)\)
\(t=0\Rightarrow0=2\cos\varphi\Rightarrow\varphi=\pm\frac{\pi}{2}\)
Vì chất điểm chuyển động theo chiều dương\(\Rightarrow\varphi< 0\Rightarrow\varphi=-\frac{\pi}{2}\)
\(\Rightarrow x=2\cos\left(\pi t-\frac{\pi}{2}\right)\)
1/ Đề bài sai, biên độ là 8 mà đi tới vị trí -10cm :D? Ủa ủa...

Hai điểm cách gần nhau nhất là: \(\dfrac{\lambda}{2}=10\Rightarrow \lambda=20cm\)
M O1 O2 d1 d2
M dao động cực đại và cách O2 xa nhất khi M nằm ở vân ngoài cùng về phía O1.
Vị trí vân cực đại này là: \([\dfrac{196}{2.20}]=4\)
\(\Rightarrow d_2-d_1=4.\lambda=4.20=80cm\)
\(\Rightarrow d_2= d_1+80=196+80=276cm\)
Chọn D
 chọn A
chọn A
Đáp án A
Dựa vào pt đề bài cho, ta tìm được x 1 m ax = 1 , 5 ( c m ) x 2 m ax = 2 ( c m ) ⇒ A 1 = 1 , 5 ( c m ) A 2 = 2 ( c m )
Mặt khác, khi x1 max thì x 2 = 0 và ngược lại nên 2 dao động này vuông pha nhau. Dễ dàng tìm được biên độ dao động tổng hợp A = A 1 2 + A 2 2 = 2 , 5 ( c m )
Lực kéo về cực đại F k v m ax = k A = m ω 2 A = 0 , 75 ( N )