Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

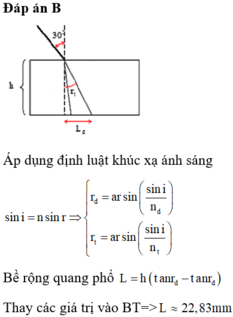
Đáp án B
+ Áp dụng định luật khúc xạ ánh sáng
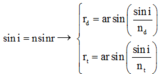
+ Bề rộng quang phổ : ![]()
→ Thay các giá trị vào biểu thức, ta thu được L = 22,83 mm.

TDHOirrtd
Áp dụng định luật khúc xạ
\(\sin i =n_t. \sin r_t\)=>\(\sin r_t = \frac{0,8}{n_t}=> r_t \approx 36,56^0\)
\(\sin i =n_d. \sin r_d\) => \(\sin r_d = \frac{0,8}{n_d}=> r_d \approx 36,95^0\)
Bề rộng quang phổ tạo ra dưới đáy bể là
\(TD = HD-HT = OH.(\tan r_d-\tan r_t) \approx 1,257 mm. \)


Vì \(\tan i\)=\(\dfrac{4}{3}\) nên i = 530
Áp dụng định luật khúc xạ cho các tia đỏ và tia tím ta có:
Với tia đỏ: sin i = nđỏ.sin rđỏ ⇒ sin 530 = 1,328.sin rđỏ ⇒ rđỏ = 36,960.
Với tia tím: sin i = ntím.sin rtím ⇒ sin 530 = 1,343.sin rtím ⇒ rtím = 36,50.
Từ hình vẽ, ta có: Độ dài vệt sáng tạo ở đáy bể là:
TĐ = HĐ – HT = IH.(tan rđỏ - tan rtím) = 1,2.(tan 36,960 – tan 36,50) = 0,015 m = 1,5 cm

Tia sáng Mặt Trời vào nước bị tán sắc và khúc xạ. Tia đỏ lệch ít nhất, tia tím lệch nhiều nhất.
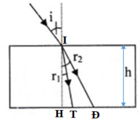
Ta có: tan i = 4/3 → i = 53,1o → sin i = 0,8
Áp dụng định luật khúc xạ tại I ta có: sin i = nđ. sin r2 = nt. sin r1
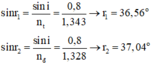
Xét tam giác vuông IHT, ta có: tan r1 = HT/IH ⇒ HT = h. tan r1
Xét tam giác vuông IHĐ, ta có: tan r2 = HĐ/IH ⇒ HĐ = h. tan r2
Độ dài quang phổ do tia sáng tạo ở đáy bể là :
ΔD = HĐ – HT = h.(tan r2 – tan r1) = 1,2.(tan 37,04o – tan 36,56o) = 0,01568m = 1,568cm

Bề rộng quang phổ liên tục bậc 3 là
\(L = x_{đỏ}^k-x_{ tím}^k= 3\frac{D}{a}(\lambda_d-\lambda_t)=2,85mm.\)
Với \(D = 2m; a= 0,8mm; \lambda_d = 0,76 \mu m; \lambda_t = 0,38 \mu m.\)

Ta có \(\dfrac{i_1}{i_2}=\dfrac{4}{5}\)
Nên chọn \(\begin{cases}i_1=4i \\ i_2=5i \end{cases}\) \(\Rightarrow i_{\equiv }=20i\)
Tại vị trí \(x_1= 0,5i_1=2i; x_2=12,5i_1=50i\)
Nên số vân trùng thỏa mãn: \(2i < k.20i < 50i\)
Có 2 giá trị k thỏa mãn là: k = 1 hoặc k = 2.
Vậy có 2 vân trùng,
Chọn đáp án B.

Đáp án C