Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu đúng: a) và g).
Câu sai: b), c), d), e), f), h).
Giải thích:
- Câu b sai vì nếu ba điểm( phân biệt) cho trước là ba điểm thẳng hàng thì có đúng 1 đường thẳng đi qua ba điểm đó.
- Câu c sai vì nếu bốn điểm ( phân biệt) cho trước là bốn điểm thẳng hàng thì có đúng 1 đường thẳng đi qua bốn điểm đó.
- Câu d sai vì hai đường thẳng phân biệt có thể song song hoặc cắt nhau.
- Câu e sai vì hai đường thẳng không cắt nhau có thể trùng nhau hoặc song song.
- Câu f sai vì hai đường thẳng không song song có thể có thể trùng nhau hoặc cắt nhau.
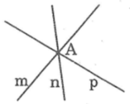
- Câu h sai vì ba đường thẳng phân biệt, đôi một cắt nhau thì có thể có đúng 1 giao điểm. Như hình vẽ dưới đây.

Mình cũng ko biết nữa ở trong sách bài tập ghi thế, mình cũng chỉ ghi lại thôi

Hai đường thẳng trùng nhau là mọi điểm chung đó
VD:ABC\
Ba điểm A,B,C thẳng hàng, ta nói hai đường thẳng Ab và BC là 2 đường thẳng trùng nhau.
Hai đường thẳng không trùng nhau còn được gọi là 2 đường thẳng phân biệt. Hai đường thẳng phân biệt hoặc chỉ có một điểm chung hoặc không có điểm chung nào.
VD: z t x y
Hai đường thẳng xy và zt không có điểm chung nào, ta nói chúng song song với nhau

Đánh số cho các điểm là 1 đến 15
Từ điểm số 15 có thể kẻ 14 đường thẳng đến 14 điểm còn lại
Từ điểm số 14 có thể kẻ 13 đường thẳng đến 13 điểm còn lại (Trừ điểm số 15 đã kẻ rồi)
.....
Từ điểm số 2 có thể kẻ 1 đường thẳng đến 1 điểm còn lại
Vậy số đường thẳng thu được là 14 + 13 + ... + 2 + 1 = 15*7 = 105

số đường thẳng thu được là:
15.(15-1):2=105 đường thẳng
mik đã viết công thức trên bài làm luôn rồi đó
Công thức: \(\frac{n.\left(n-1\right)}{2}\)
Với bài toán này ta có: \(\frac{15.\left(15-1\right)}{2}\)
= 105
Vậy số đường thẳng thu được là: 105 đường thẳng
a) sai; b) sai; c) sai; d) đúng; e) sai