Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGFAGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGFAGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG

- Có 5 cách chọn chữ số hàng trăm.
- Có 5 cách chọn chữ số hàng chục.
- Có 4 cách chọn chữ số hàng đơn vị.
Số số được tạo thành là:
\(5.5.4=100\) (số)
Tuy nhiên trong 100 số này đã bị mất đi 1 số số chẵn:
| 012 | 013 | 014 | 015 |
| 021 | 023 | 024 | 025 |
| 031 | 032 | 034 | 035 |
| 041 | 042 | 043 | 045 |
| 051 | 052 | 053 | 054 |
Vậy số số lẻ hơn số số chẵn là 8 số.
Có số số chẵn là:
\(\left(100-8\right):2=46\) (số)
Có số số lẻ là :
\(100-46=54\) (số)
Nếu coi 100 số là 100 %.
Xác xuất chọn được số chẵn ở lần chọn đầu là:
\(46:100.100=46\%\)
Xác xuất chọn được số chẵn ở lần chọn thứ 2 (nếu lần ko trúng) là:
\(46:99.100\approx46,5\)

Xếp A và B cạnh nhau: 2 cách
Coi cặp AB như 1 bạn, kết hợp 8 bạn còn lại, có \(9!\) cách hoán vị
Xác suất: \(P=\dfrac{9!.2}{10!}=\dfrac{1}{5}\)

Đáp án A
Chọn 10 tấm bất kỳ có: C 30 10 , trong 30 thẻ có 15 thẻ mang số chẵn, 15 thẻ mang số lẻ và 3 số chia hết cho 10.
Ta chọn 10 tấm thẻ lấy ra 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó chỉ có một tấm mang số chia hết cho 10 có: C 15 5 . C 3 1 . C 12 4 cách
Do đó xác suất cần tìm là: C 15 5 . C 3 1 . C 12 4 C 30 10 = 99 667 .

Đáp án D
Chon 3 số bất kì có C 10 3 = 120 cách
TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp có 8 cách
TH2: 3 số chọn ra là 2 số tự nhiên liên tiếp
+) 3 số chọn ra có cặp (1;2) hoặc (9;10) có 2.7 = 14 cách
+) 3 số chọn ra có cặp ( 2 ; 3 ) ; ( 3 ; 4 ) ; . . . . ( 8 ; 9 ) có 6.6 = 36 cách
Vậy xác suất cần tìm là
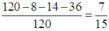




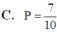



Chọn C
Số cách chọn của An là C 10 3 ; số cách chọn của Bình là C 10 3 . Vậy số phần tử của không gian mẫu là: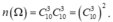
Gọi A là biến cố “ Hai bộ ba số An và Bình chọn ra có nhiều nhất một số giống nhau”.
TH1: Không có số nào giống nhau thì có C 10 3 C 7 3 cách chọn.
TH2: Có một số giống nhau thì có C 10 3 C 3 1 C 7 2 cách chọn.
Do đó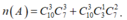
Vậy xác suất cần tìm là: