Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy cuộn dây không thuần cảm vì : U 2 ≠ U A M 2 + U N B - U M N 2

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng

Chọn D.
U = U R 2 + U L − U C 2 = 13 2 + 13 − 65 2 = 13 17 ≠ U
để cho cuộn dây có trở kháng r
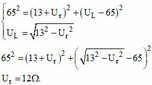
k = cos φ = U R + U r U = 13 + 12 65 = 5 13 .

Theo bài ra ta có
U 2 = U R 2 + U C - U L 2
![]()
cos φ = R/Z = U R /U = 40/50 = 0,8

Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)

Đáp án C
+ Giả sử cuộn dây có điện trở thuần 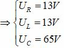
+ Ta có: ![]()
=> Cuộn dây có điện trở r
![]()

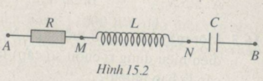
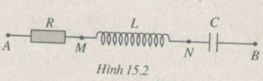

Ta vẽ giản đồ vectơ : U → = U A M → + U M N → + U N B →
Trong đó U A M → ↑ ↑ I → ; U N B → ⊥ I →
Hai tam giác ABM và NBM bằng nhau (có các cạnh lần lượt bằng nhau) dẫn tới kết quả hai tam giác vuông HAB và HNM đồng dạng, suy ra
⇒ tan β = 16/65 = 1/5
Trên Hình 15.1.G
2 β = φ 1
⇒ sin φ 1 = sin2 β
Mặt khác theo Hình 15.1G, ta có :
φ + φ1 = π/2 ⇒ cosφ = sinφ1 = 5/13