Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dòng điện đổi chiều khi dòng điện đi qua VTCB.
Vẽ đường tròn tương ứng
-60 x 0 N M 150
Vị trí ban đầu ứng với pha ban đầu là \(-\frac{\pi}{3}\) ứng với điểm N.
Vị trí gần nhất (quay theo chiều ngược chiều kim đồng hồ) thì điểm N là vị trí gần nhất tại đó dòng đổi chiều.
\(t=\frac{\varphi}{\omega}=\frac{5\pi}{6}\Rightarrow\omega=\frac{5\pi}{6}:t=2\pi.10^6\)
Điện tích cực đại \(Q_o=\frac{I_0}{\omega}=\frac{30}{2\pi.10^6}=\frac{1,5.10^{-5}}{\pi}C\)
Như vậy đáp án C thỏa mãn.

Áp dụng công thức tính năng lượng điện từ trường ta có
W = Wđ = Wt \(\Rightarrow\frac{1}{2}LI_0^2=\frac{1}{2}lI^2+\frac{1}{2}Cu^2\)
\(\Rightarrow u=\sqrt{\left(I_0^2-I^2\right)\frac{L}{C}}\Rightarrow u=\)\(\sqrt{\frac{0,1}{10^{-5}}\left(0,05^2-0,02^2\right)}=4\left(V\right)\)
chọn A

mình bị nhầm ở đáp án
A. \(\frac{4}{3}\mu s\) các câu khác cũng như vậy nhé
Năng lượng của mạch dao động W = \(\frac{Q_0^2}{2C}=\frac{LI^2_0}{2}\) → chu kì dao động của mạch
\(T=2\pi\sqrt{LC}=2\pi\frac{Q_0}{I_0}=16.10^{-6}\left(s\right)=16\mu s\).Thời gian điện tích giảm từ Q0 dến Q0/2
q = Q0cos \(\frac{2\pi}{T}t=\frac{Q_0}{2}\rightarrow\frac{2\pi}{T}t=\frac{\pi}{3}\rightarrow t=\frac{T}{6}=\frac{8}{3}\mu s\)
→ C

Ta có : \(\frac{T_{W_{\text{đ}}}}{6}=1,5.10^{-4}\)
\(\Rightarrow\frac{T_q}{6}=\frac{2T_{W_{\text{đ}}}}{6}=3.10^{-4}\)
Vậy chọn D.

- Tại t = 0, i = 0,5I0 và đang tăng, dòng điện đổi chiều khi i = 0 A, tương ứng với:
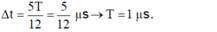
- Điện tích cực đại trên bản tụ:
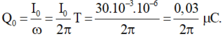

Điện tích trên tụ giảm từ cực đại xuống nửa cực đại là \(\dfrac{T}{6}=2.10^-4s\Rightarrow T = 12.10^{-4} s\)
Năng lượng điện giảm từ cực đại xuống nửa cực đại ứng với điện tích giảm từ \(Q_0\) (cực đại) xuống \(\dfrac{Q_0}{\sqrt 2}\)
Biểu diễn bằng véc tơ quay ta thấy véc tơ quay đã quay \(45^0\), ứng với thời gian là: \(\dfrac{T}{8}=1,5.10^{-4}s\)
Chọn A

Sử sụng hệ thức: 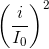 +
+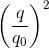 = 1
= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω = 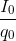 = 50 (rad/s)
= 50 (rad/s)

Cách 1: Trong 5 μs = T/4 nên điện tích dịch chuyển là Q0
Số \( Ne = \frac{Q_0}{e} \text{ với } Q_0 = \frac{I_0}{\omega }\)
Đáp án A
Cách 2: Áp dụng \(q = n.e = \int_{0}^{5.10^{-6}} 0,012.\sin (10^5 \pi t) dt = 3,82.10^{-8}C \Rightarrow n = \frac{q}{e } = \frac{3,82.10^{-8}}{1,6.10^{-19}} = 2,39.10^{11}\)
Đáp án A

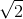
Chọn đáp án C