OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

Tham gia ngay Cuộc thi "Đi tìm Đại sứ OLM" giải thưởng tới 10 triệu đồng

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
NT
Nguyễn Thị Thùy
15 tháng 10 2016 - olm

Làm tính chia:

a, 258 : 512

b, 4x2(y + z)5 : 2x(y + z)3

c, \(\frac{3}{4}\left(x+2\right)^{2n}.\left(x-3\right)^{n-2}:\frac{2}{3}\left(x+2\right)\left(x-3\right)\)

d, \(\left(\frac{-10}{3}x^2yz^3+\frac{15}{2}xy^3z^4-5xyz^2\right):\frac{5}{3}xyz^2\)
#Toán lớp 8
0
CG
Cố gắng hơn nữa
13 tháng 7 2016 - olm

các bạn cho mình hỏi cái này với:

Cho x+y=a và \(x^2+y^2=b\)

tính giá trị của M= \(x^3+y^3+x^4+y^4\)

giờ ta đặt ra tính đơn lẻ là

\(x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)\)

\(x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2\)

vậy thì giờ làm cách nào hay có thể rút \(xy=\frac{a^2-b}{2}\)được hay không
#Toán lớp 8
0
DQ
Diễm Quỳnh
6 tháng 10 2020

Bài 8 : Tính giá trị biểu thức 16x2 - 24x+ 9 trong mỗi trường hợp sau

a. x=0

b. x=1/4

c. x= 12

d. x= 3/4

Bài 9: Tính

a. ( 2x - 3)2

b. (5/4 -x)2

c. ( 2x + 3y)2

d. ( 3x+ 2/3 yz )2

e. ( xy/2 - xy/3) ( xy/2 + xy/3)

f. ( 2x - y + z )2
#Toán lớp 8
1
TT
Thu Thao
6 tháng 10 2020

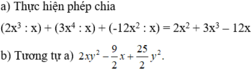
a, Đặt \(A=16x^2-24x+9\)

⇒ \(A=(4x-3)^2\)

Vs x = 0

=> A = \((-3)^2=9\)

Vs \(x=\frac{1}{4}\)

⇒ \(A=\left(1-3\right)^2=4\)

Vs \(x=12\)

=> \(A=\left(48-3\right)^2=45^2=2025\)

Vs \(x=\frac{3}{4}\)

⇒ A = 0

2.

a, \(=4x^2-12x+9\)

b, \(=\frac{25}{16}-\frac{5}{2}x+x^2\)

c, \(=4x^2+12xy+9y^2\)

d, \(=9x^2+4xyz+\frac{4}{9}y^2z^2\)

e, \(=\left(\frac{x^2y^2}{4}-\frac{x^2y^2}{9}\right)\) (bỏ ngoặc hộ mình nhé <3)

f, \(=4x^2+y^2+z^2-4xy+4xz-2yz\)

Đúng(0)
N
nhidethuong123456
25 tháng 7 2018

a)(x-5)\(^2\)-16

b)25-(3-x)\(^2\)

c)49(y-4)\(^2\)-9(y+2)\(^2\)

d)11x+11y-x\(^2\)-xy

e)x\(^2\)-xy-8x+8y
#Toán lớp 8
4
HH
Hắc Hường
30 tháng 7 2018

Giải:

a) \(\left(x-5\right)^2-16\)

\(=\left(x-5-4\right)\left(x-5+4\right)\)

\(=\left(x-9\right)\left(x-1\right)\)

b) \(25-\left(3-x\right)^2\)

\(=\left(5-3+x\right)\left(5+3-x\right)\)

\(=\left(2+x\right)\left(8-x\right)\)

c) \(49\left(y-4\right)^2-9\left(y+2\right)^2\)

\(=\left[7\left(y-4\right)\right]^2-\left[3\left(y+2\right)\right]^2\)

\(=\left[7\left(y-4\right)-3\left(y+2\right)\right]\left[7\left(y-4\right)+3\left(y+2\right)\right]\)

\(=\left(7y-28-3y-6\right)\left(7y-28+3y+6\right)\)

\(=\left(4y-34\right)\left(10y-22\right)\)

d) \(11x+11y-x^2-xy\)

\(=11\left(x+y\right)-x\left(x+y\right)\)

\(=\left(11-x\right)\left(x+y\right)\)

e) \(x^2-xy-8x+8y\)

\(=x\left(x-y\right)-8\left(x-y\right)\)

\(=\left(x-8\right)\left(x-y\right)\)

Vậy ...

Đúng(0)
BM
Bùi Mạnh Khôi
30 tháng 7 2018

\(\left(x-5\right)^2-16\)

\(=\left(x-5\right)^2-4^2\)

\(=\left(x-5-4\right)\left(x-5+4\right)\)

\(=\left(x-9\right)\left(x-1\right)\)

\(25-\left(3-x\right)^2\)

\(=5^2-\left(3-x\right)^2\)

\(=\left(5+3-x\right)\left(5-3+x\right)\)

\(=\left(8-x\right)\left(2+x\right)\)

\(49\left(y-4\right)^2-9\left(y+2\right)^2\)

\(=7^2\left(y-4\right)^2-3^2\left(y+2\right)^2\)

\(=\left[7\left(y-4\right)\right]^2-\left[3\left(y+2\right)\right]^2\)

\(=\left(7y-28\right)^2-\left(3y+6\right)^2\)

\(=\left(7y-28-3y-6\right)\left(7y-28+3y+6\right)\)

\(=\left(4y-34\right)\left(10y-22\right)\)

Đúng(0)
K
Kaijo
16 tháng 3 2020 - olm
8,Thực hiện phép...
Đọc tiếp

8,Thực hiện phép tính

a,\(\frac{5x^2-y^2}{xy}-\frac{3x-2y}{y}\)

b,\(\frac{3}{2x+6}-\frac{x-6}{2x^2+6x}\)

c,\(\frac{2x}{x^2+2xy}+\frac{y}{xy-2y^2}+\frac{4}{x^2-4y^2}\) 

d,\(\frac{1}{x-y}+\frac{3xy}{y^3-x^3}+\frac{x-y}{x^2+xy+y^2}\) 

e,\(\frac{2x+y}{2x^2-xy}+\frac{16x}{y^2-4x^2}+\frac{2x-y}{2x^2+xy}\) 

f,\(\frac{1}{1-x}+\frac{1}{1+x}+\frac{2}{1+x^2}+\frac{4}{1+x^4}+\frac{8}{1+x^8}+\frac{16}{1+x^{16}}\)
#Toán lớp 8
0
DT
Dương Thị Thu Trà
8 tháng 7 2016

Rút gọn và tính giá trị của biểu thức tại x = -1,76 và y = 3/25

\(P=\left[\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{4x^4+4x^2y+y^2-4}{x^2+y+xy+x}\right]:\frac{x+1}{2x^2+y+2}\)
#Toán lớp 8
1
VD
Võ Đông Anh Tuấn
8 tháng 7 2016

\(P=\left[\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{4x^4+4x^2y+y^2-4}{x^2+y+xy+x}\right]:\frac{x+1}{2x^2+y+2}\)

\(P=\left[\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{\left(x+y\right)\left(x-2y\right)}\right):\frac{\left(2x^2+y+2\right)\left(2x^2+y-2\right)}{\left(x+y\right)\left(x+1\right)}\right]:\frac{x+1}{2x^2+y+2}\)

\(P=\left(\frac{\left(x-y\right)\left(x+y\right)+x^2+y^2+y-2}{\left(x+y\right)\left(2y-x\right)}.\frac{\left(x+y\right)\left(x+1\right)}{\left(2x^2+y+2\right)\left(2x^2+y-2\right)}\right):\frac{2x^2+y+2}{x+1}\)

\(P=\left(\frac{2x^2+y-2}{2y-x}.\frac{x+1}{2x^2+y-2}\right).\frac{1}{x+1}\)

\(P=\frac{1}{2y-x}\)

Tại \(x=-1,76\) và \(y=\frac{3}{25}\) thì giá trị của \(Q=\frac{1}{2}\)

 

Đúng(0)
DT
Dương Thị Thu Trà
8 tháng 7 2016

thanks hihi

Đúng(0)
SG
Sách Giáo Khoa
28 tháng 4 2017
Thực hiện các phép tính...
Đọc tiếp

Thực hiện các phép tính :

a) \(\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{3x+9}\right)\)

b) \(\left(\dfrac{2}{x-2}-\dfrac{2}{x+2}\right).\dfrac{x^2+4x+4}{8}\)

c) \(\left(\dfrac{3x}{1-3x}+\dfrac{2x}{3x+1}\right):\dfrac{6x^2+10x}{1-6x+9x^2}\)

d) \(\left(\dfrac{x}{x^2-25}-\dfrac{x-5}{x^2+5x}\right):\dfrac{2x-5}{x^2+5x}+\dfrac{x}{5-x}\)

e) \(\left(\dfrac{x^2+xy}{x^3+x^2y+xy^2+y^3}+\dfrac{y}{x^2+y^2}\right):\left(\dfrac{1}{x-y}-\dfrac{2xy}{x^3-x^2y+xy^2-y^3}\right)\)
#Toán lớp 8
1
NT
Nguyen Thuy Hoa
24 tháng 6 2017

Phân thức đại số

Phân thức đại số

Đúng(0)
KU
KCシ ᙅᖺủ Ʈịᙅᖺ Vℓ๏ǥs ︵²ᵏ⁸
25 tháng 7 2021 - olm

\(a.\left(5x^4-3x^3+x^2\right):3x^2=\frac{5}{3}x^2-x+\frac{1}{3}\)

\(b.\left(5xy^2+9xy-x^2y^2\right):\left(-xy\right)=-5y-9+xy\)

\(c.\left(x^3y^3-x^2y^3-x^3y^2\right):x^2y^2=xy-y-x\)
#Toán lớp 8
1
NH
Nguyễn Huy Tú
25 tháng 7 2021

a, mình nghĩ đề là cm đẳng thức nhé 

\(VT=\left(5x^4-3x^3+x^2\right):3x^2=\frac{5x^4}{3x^2}-\frac{3x^3}{3x^2}+\frac{x^2}{3x^2}=\frac{5}{3}x^2-x+\frac{1}{3}=VP\)

Vậy ta có đpcm 

b, \(VT=\left(5xy^2+9xy-x^2y^2\right):\left(-xy\right)=\frac{5xy^2}{-xy}+\frac{9xy}{-xy}-\frac{x^2y^2}{-xy}\)

\(=-5y-9+xy=VP\)

Vậy ta có đpcm 

c, \(VT=\left(x^3y^3-x^2y^3-x^3y^2\right):x^2y^2=\frac{x^3y^3}{x^2y^2}-\frac{x^2y^3}{x^2y^2}-\frac{x^3y^2}{x^2y^2}=xy-y-x=VP\)

Vậy ta có đpcm 

Đúng(0)
A
Arons
8 tháng 8 2019

Rút gọn:

a) \(\frac{x^3+2x^2+1}{4x^2-4}.\frac{x+2}{x^2+1}.\frac{2x^2-2}{x^3+2x^2+1}\)

b)\(\frac{x^4-y^4}{x^2+y^2-2xy}.\frac{x-y}{xy+x^2}\)

c)\(\frac{x^2-9}{x+5}.\frac{2x}{x+3}+\frac{x^2-9}{x+5}.\frac{5-x}{x+3}\)
#Toán lớp 8
0
N
Neoneo
24 tháng 6 2018 - olm

Tính giá trị biểu thức : 
a) \(\frac{9}{25}x^2+\frac{12}{35}xy+\frac{4}{49}y^2\) Tại x = 5 ; y =-7
b) \(\frac{25}{16}u^4v^2+\frac{1}{5}u^2v^3+\frac{4}{625}v^4\) Tại u = \(\frac{2}{5}\); v = 5
#Toán lớp 8
1
NT
nguyễn thị huyền anh
24 tháng 6 2018

a,\(=\left(\frac{3}{5}x+\frac{2}{7}y\right)^2=\left(\frac{3}{5}.5+\frac{2}{7}.\left(-7\right)\right)^2=0\)

\(b,=\left(\frac{5}{4}u^2v+\frac{2}{25}v^2\right)^2=\left(\frac{5}{4}.\left(\frac{2}{5}\right)^2.5+\frac{2}{25}.5^2\right)^2=3^2=9\)

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP