Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Suất điện động cực đại: \(E_0=\omega.N.BS=\omega N \phi_0\)
Vậy giá trị hiệu dụng: \(E=\dfrac{E_0}{\sqrt 2}=0,5\sqrt 2.\omega.N.\phi_0\)
Suất điện động cảm ứng trong khung: \(e=-\phi'_{(t)}\)
\(\Rightarrow e=14,4.\sin(720t+\dfrac{\pi}{6})(V)\)
\(e=E_0\cos\left(\omega t+\frac{\pi}{2}\right)=E_0\sin\left(\omega t+\pi\right)\)
Pha ban đầu theo hàm sin là góc tạo bỏi véc tơ pháp tuyến mặt phẳng khung dây và véc tơ cảm ứng từ.
Suy ra: \(\alpha=\pi\)(rad)
a. Từ thông qua khung dây
\(\Phi_0=NB_0S_{khung}=1.0.01.25.10^{-4}=25.10^{-6}Wb\)
Từ thông và cảm ứng từ cùng pha với nhau
\(\phi=\Phi_0\sin100\pi t\left(Wb\right)=25.10^{-6}\sin100\pi t.\)
b. Suất điện động
\(e=-\phi'=-25.10^{-6}.100\pi\cos100\pi t=25.10^{-4}\pi\sin\left(100\pi t-\frac{\pi}{2}\right)V.\)
\(E_0=25.10^{-4}\pi V.\)
c. Cường độ dòng điện
Do khung dây hình vuông có diện tích 25 cm^2 nên cạnh hình vuông là 5cm tức là chu vi của hình vuông là 4x5 = 20cm đây chính là chiều dài của sợi dây đồng đem quấn.
điện trở của sợi đồng là \(R=\frac{\rho l}{S}=\frac{1,72.10^{-4}.20.10^{-2}}{1.10^{-4}}=0.344\Omega.\)
\(i=\frac{e}{r}=\frac{E_0}{r}\sin\left(100\pi t-\frac{\pi}{2}\right)A\)
\(=\frac{25.10^{-4}\pi}{0.344}\sin\left(100\pi t-\frac{\pi}{2}\right)A=0.0228\sin\left(100\pi t-\frac{\pi}{2}\right)A.\)
\(I_0=0,0228A.\)
Sử sụng hệ thức: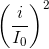 
+
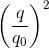= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =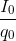 
= 50 (rad/s)
Khi tăng điện dung nên 2.5 lần thì dung kháng giảm 2.5 lần. Cường độ dòng trễ pha hơn hiệu điện thế $\pi/4$ nên
$Z_L-\frac{Z_C}{2.5}=R$
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì $Z_LZ_C=R^2+Z_L^2$
$Z_LZ_C=(Z_L-\frac{Z_C}{2.5})^2+Z_L^2$
Giải phương trình bậc 2 ta được: $Z_C=\frac{5}{4}Z_L$ hoặc $Z_C=10Z_L$(loại vì Zl-Zc/2.5=R<0)
$R=\frac{Z_L}{2}$
Vẽ giản đồ vecto ta được $U$ vuông góc với $U_{RL}$ còn $U_C$ ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi $U_L$ và $U_{LR}$
$\tan\alpha=\frac{R}{Z_L}=0.5$
$\sin\alpha=1/\sqrt5$
$U=U_C\sin\alpha=100V$
\(U_{C}{max}=\frac{U\sqrt{R^{2}+Z_L^{2}}}{R}\); \(Zc=\frac{R^{2}+Z_L^{2}}{Z_L}\)
khi C2=2,5C1---->Zc2=Zc1/2,5=ZC/2,5
do i trể pha hơn U nên Zl>Zc/2,5
\(\tan\frac{\pi }{4}=\frac{Z_L-0,4Zc}{R}=1\Rightarrow R=Z_L-0,4Z_C\)
\(\Rightarrow Z_C.Z_L=Z_L^{2}+(Z_L-0,4Z_C)^{2}\Rightarrow 2Z_L^{2}-1,8Z_CZ_L+0,16Z_C^{2}=0\Rightarrow Z_L=0,8Z_C;Z_L=0,1Z_C\)(loai)
\(\Rightarrow R=Z_L-1,25.0,4Z_L=0,5Z_L\)
\(\Rightarrow U_{C}{max}=\frac{U\sqrt{Z_L^{2}+0,25Z_L^{2}}}{0,5Z_L}=100\sqrt{5}\Rightarrow U=100V\)
Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)
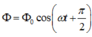
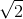
Đáp án A
Do đó suy ra pha của e là φ = 0.