
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y
Theo đề bài ta có x = \(\frac{a}{m}\), y = \(\frac{b}{m}\)(a, b, m ∈ Z, b # 0)
Vì x < y nên ta a < b
Ta có: x = \(\frac{2a}{2m}\), y = \(\frac{2b}{2m}\); z = \(\frac{a+b}{2m}\)
Vì a < b \(\Rightarrow\) a + a < a + b \(\Rightarrow\) 2a < a + b
Vì 2a < a + b nên x < z (1)
Vì a < b \(\Rightarrow\) a + b < b + b \(\Rightarrow\) a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta \(\Rightarrow\) x < z < y

đây là cậu chép trg chỗ giải đáp rồi mà mk ko đc lm giống trg giải đáp

a) Thiếu ĐK: \(a+b+c=0\)
Giải:
Ta có:
\(a^3+a^2c-abc+b^2c+b^3\)
\(=a^3+a^2c+a^2b-a^2b-abc+b^2c+b^3+b^2a-b^2a\)
\(=a^2\left(a+b+c\right)-a^2b-abc+b^2\left(a+b+c\right)-b^2a\)
\(=-a^2b-abc-b^2a\)
\(=-ab\left(a+b+c\right)\)
Mà \(a+b+c=0\) nên:
\(=-ab.0\)
\(=0\)
Vậy \(a^3+a^2c-abc+b^2c+b^3=0\) (Đpcm)

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow ad=bc\)
Nếu:
\(\dfrac{a+b}{a}=\dfrac{c+d}{c}\Leftrightarrow c\left(a+b\right)=a\left(c+d\right)\)
\(ac+bc=ac+ad\)
\(bc=ad\)
\(\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\rightarrowđpcm\)
Đặt \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)=k
=> a=k.b ; c=k.d
Ta có :
\(\dfrac{a+b}{a}\)=\(\dfrac{b.k+b}{b}\)=\(\dfrac{b.\left(k+1\right)}{b}\)=k+1 ( 1 )
\(\dfrac{c+d}{c}\)=\(\dfrac{d.k+d}{d}\)=\(\dfrac{d.\left(k+1\right)}{d}\)=k+1 ( 2 )
Từ (1) và (2) thì : \(\dfrac{a+b}{a}\)=\(\dfrac{c+d}{c}\)

Hoàng Anh Thư mk nghĩ x = \(\frac{a}{m}\) , như tkế mk làm đc , còn như x = \(\frac{a}{b}\) tkì mk chịu thôi !!
![]()

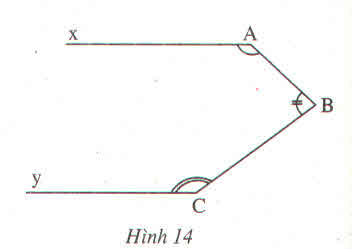



Ở trong góc AOB vẽ tia O t / / A x . Khi đó A O t ^ = A ^ = a ° (cặp góc so le trong).
Suy ra B O t ^ = b ° . Vậy B O t ^ = B ^ = b ° .
Do đó By // Ot (vì có cặp góc so le trong bằng nhau).
Vậy Ax // By (vì cùng song song với Ot)