Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để cho 3 cái đều có diện tích là \(\frac{1}{3}ABC\) thì :
Trước tiên ta nối AD. Ta được SABC=SADC=1/2 SABC
Để vẽ được BED bằng 1/3 SABC thì ta vẽ SBED= \(\frac{1}{3}:\frac{1}{2}\left(S_{ABD}\right)=\frac{2}{3}S_{ABD}\) hay còn nói : BE=2/3 BA
Tương tự với tam giác GDC
Phần còn lại là tứ giác và cũng bằng 2 tam giác kia

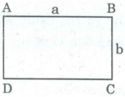
* Xét hình chữ nhật ABCD có chiều dài AB = a, chiều rộng AD = b.
Ta có: S A B C D = ab.
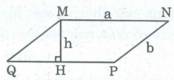
* Hình bình hành MNPQ có góc M là góc tù, MN = a, cạnh MQ = b
Kẻ đường cao MH. Ta có: S M N P Q = MH.a
Theo bài ra, ta có: MH.a = 1/2 ab
Suy ra: MH = 1/2 b hay MH = MQ/2
Tam giác MHQ vuông tại H và MH = MQ/2
Cạnh đối diện góc nhọn bằng một nửa cạnh huyền nên ∠ (MQH) = 30 0
Vậy góc nhọn của hình bình hành bằng 30 0 .

gọi a và b lần lượt là chiều dài và chiều rộng của hình chữ nhật.
ta có :2(a+b)=20
a*b =24
=>a=6;b=4
vậy ........................
Gọi chiều dài và chiều rộng hình chữ nhật đó là $a$ và $b$ ($a>b>0;cm$)
Do hình chữ nhật có chu vi là $20$ cm nên có:
$2.(a+b)=20$
$⇒a+b=10$
Hình chữ nhật có diện tích $24cm^3$ nên có:
$ab=24$
Suy ra ta có hệ phương trình $\begin{cases}a+b=10\\ab=24\end{cases}$
$⇔\begin{cases}a=10-b\\(10-b)b=24\end{cases}$
$⇔\begin{cases}a=10-b\\b^2-10b+24=0\end{cases}$
$⇔\begin{cases}a=10-b\\(b-4)(b-6)=0\end{cases}$
$⇔\begin{cases}a=10-b\\\(\left[{}\begin{matrix}b=4\\b=6\end{matrix}\right.\)\end{cases}$
Với $b=4⇒a=10-4=6(cm)$
$b=6⇒a=10-6=4(cm)$
Mà $a>b>0⇒a=6(cm);b=4(cm)$
Vậy hình chữ nhật đó có chiều dài chiều rộng lần lượt là $6;4(cm)$

Gọi chiều dài HCN thứ nhất là : x ( x > 0 ; m)
Chiều rộng HCN thứ nhất là : x - 9 ( m)
Diện tích HCN thứ nhất là : x( x - 9) ( m2)
Chiều dài HCN thứ hai là : x + 15 ( m)
Chiều rộng HCN thứ hai là : x - 9 + 5 = x - 4 ( m)
Diện tích HCN thứ hai là : ( x - 4)( x + 15) ( m2)
Theo đề bài , ta có phương trình sau :
( x - 4)( x + 15) - x( x - 9) = 640
⇔ x2 + 11x - 60 - x2 + 9x = 640
⇔ 20x = 700
⇔ x = 35 ( TM ĐK)
Chiều rộng HCN thứ nhất là : 35 - 9 = 26 ( m)
Chiều dài HCN thứ hai là : 35 + 15 = 50 (m)
Chiều rộng HCN thứ hai là : 35 - 4 = 31 ( m)
KL....
#)Giải :
Gọi chiều dài hình chữ nhật thứ nhất là x ( x > 0 ; m )
=> Chiều rộng hình chữ nhật thứ nhất là x - 9 ( m )
=> Diện tích hình chữ nhật thứ nhất là x( x - 9 ) ( m2)
=> Chiều dài hình chữ nhật thứ hai là x + 15 ( m )
=> Chiều rộng hình chữ nhật thứ hai là x - 9 + 5 = x - 4 ( m )
=> Diện tích hình chữ nhật thứ hai là ( x - 4 )( x + 15 ) ( m2)
Theo đề bài, ta có phương trình sau :
( x - 4 )( x + 5) - x( x - 9) = 640
<=> x2 + 11x - 60 - x2 + 9x = 640
<=> 20x = 700
<=> x = 35 ( thỏa mãn điều kiện )
=> Chiều rộng hình chữ nhật thứ nhất là : 35 - 9 = 26 ( m )
=> Chiều dài hình chữ nhật thứ nhất là : 35 + 15 = 50 ( m )
=> Chiều rộng hình chữ nhật thứ hai là : 35 - 4 = 31 ( m )
Vậy ....................................................................................

Ta có: Diện tích hình bình hành = đ.c trong đó (đ: độ dài đáy, c: chiều cao)
Lại có: Hình bình hành nội tiếp hình chữ nhật và diện tích hình chữ nhật = chiều dài . chiều rộng
\(\Rightarrow\) Shbh \(\le\) Shcn
Dấu "=" xảy ra \(\Leftrightarrow\) Shbh = Shcn \(\Leftrightarrow\) đ.c = d. r = 20 . 30 = 600 (cm2)
Vậy Shbh đạt Max \(\Leftrightarrow\) Shbh = Shcn = 600 cm2
Chúc bn học tốt!