Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
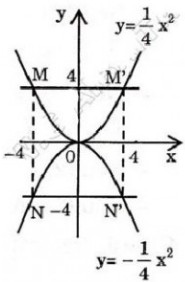
Đồ thị nằm ở phía trên trục hoành
- Các cặp điểm A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm thấp nhất của đồ thị.
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5.
Bài giải:
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5
(đơn vị đo trên các trục tọa độ là xentimet)
Lời giải:
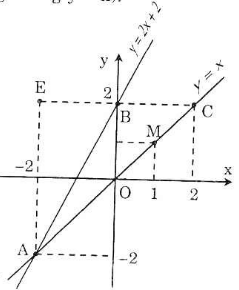
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x. Vẽ đường thẳng qua B(0; 2) và E(-1; 0) được đồ thị hàm số y = 2x + 2.
b) Tìm tọa độ của điểm A: giải phương trình 2x + 2 = x, tìm được x = -2. Từ đó tìm được x = -2, từ đó tính được y = -2, ta có A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
a) Đồ thị hàm số \(y=x\) là 1 đường thẳng đi qua 2 điểm O \(\left(0;0\right)\) và E\(\left(1;1\right)\)
Đồ thị hàm số \(y=2x+2\) là 1 đường thẳng đi qua 2 điểm B \(\left(0;2\right)\) và D \(\left(-1;0\right)\)
b) Hoành độ giao điểm A của 2 đường thẳng đã cho là nghiệm của pt:
\(x=2x+2\)
\(\Leftrightarrow\) \(x-2x=2\)
\(\Leftrightarrow\) \(-x=2\)
\(\Leftrightarrow\) \(x=-2\)
Tại \(x=-2\) thì giá trị của y là: \(y=2.\left(-2\right)+2=-2\)
Vậy tọa độ điểm A \(\left(-2;-2\right)\)
c) Đường thẳng song song với trục tung Ox và cắt trục hoành tại điểm B(0;2)
\(\Rightarrow\) Suy ra phương trình đường thẳng có dạng \(y=2x\)
Hoành độ giao điểm C của 2 đường thẳng y=2x và y=x là nghiệm của pt: 2x=x
\(\Rightarrow\) Tọa độ điểm C (2;2)
\(S_{ABC}=S_{ADO}+S_{BCOD}\)
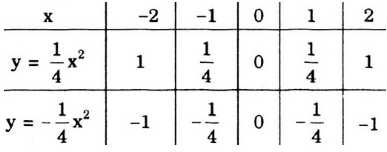
a) Vẽ đồ thị
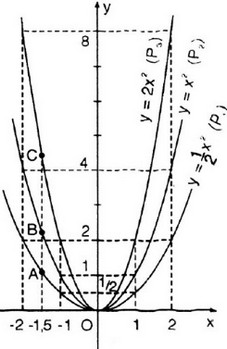
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = 
. (-1,5)2 = . 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 = . 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.
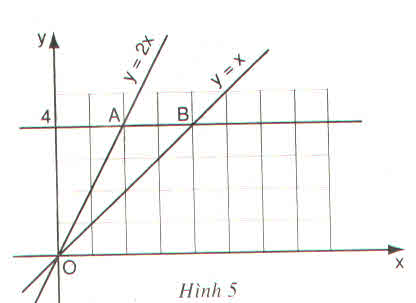
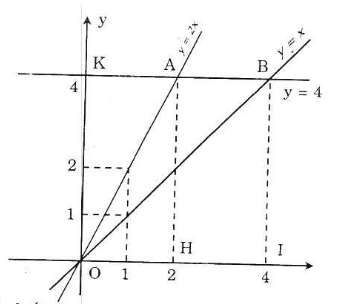
a) Xem hình trên
b) A(2; 4), B(4; 4).
Tính chu vi ∆OAB.
Dễ thấy AB = 4 - 2 = 2 (cm).
Áp dụng định lý Py-ta-go, ta có:
OA =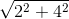 
= 2√5 (cm), OB = 
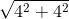= 4√2 (cm).
Tính diện tích ∆OAB.
Gọi C là điểm biểu diễn số 4 trên trục tung, ta có:
= 
- 
= 
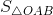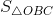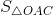OC . OB - OC . AC.
= . 42 - . 4 . 2 = 8 - 4 = 4 (cm2).
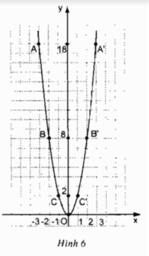
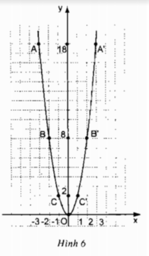
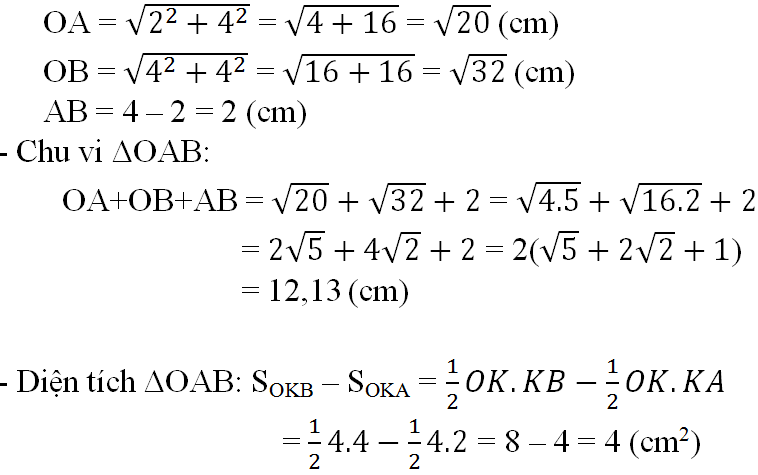
Đồ thị nằm ở phía trên trục hoành
- Các cặp điểm A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm thấp nhất của đồ thị.