Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

△OAB ∼ △OA'B' (g-g) \(=>\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=>\dfrac{d}{d'}=\dfrac{h}{h'}\left(1\right)\)
△FOI ∼ △FA'B' (g-g) \(=>\dfrac{OF}{FA'}=\dfrac{OI}{A'B'}\)
mà FA' = OA' - OF; OI = AB
\(=>\dfrac{OF}{OA'-OF}=\dfrac{AB}{A'B'}=>\dfrac{f}{d'-f}=\dfrac{h}{h'}\left(2\right)\)
từ (1)(2) \(=>\dfrac{d}{d'}=\dfrac{f}{d'-f}=>dd'-df=d'f\)
\(=>dd'-d'f=df=>d'\cdot\left(d-f\right)=df\\ =>d'=\dfrac{df}{d-f}=\dfrac{24\cdot16}{24-16}=48\left(cm\right)\left(3\right)\)
thay (3) vào (1) ta được: \(\dfrac{24}{48}=\dfrac{2}{h'}\)
\(=>h'=\dfrac{2\cdot48}{24}=4\left(cm\right)\)
vậy khoảng cách từ ảnh đến thấu kính là 48 cm; chiều cao ảnh là 4cm

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{15}{30}\Rightarrow h'=4cm\)

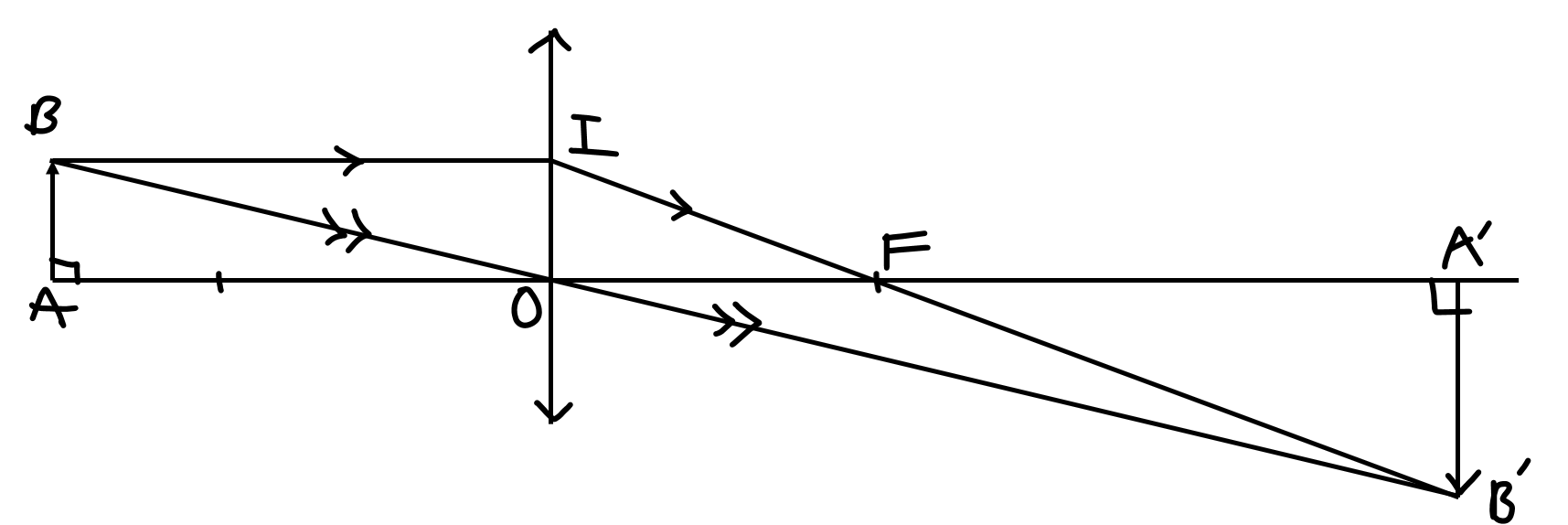
Ảnh của một vật sáng AB có dạng mũi tên đặt vuông góc với trục chính của thấu kính
Muốn dựng ảnh A’B’ của AB qua thấu kính, chỉ cần dựng ảnh B’ của B bằng cách vẽ đường truyền của hai tia sáng đặc biệt, sau đó từ B’ hạ vuông góc xuống trục chính ta có ảnh A’ của A.
a) Trường hợp tạo ảnh thật

b) Trường hợp tạo ảnh ảo

Ảnh của một điểm sáng S tạo bởi thấu kính hội tụ
Từ S ta vẽ đường truyền của hai trong ba tia đặc biệt đến thấu kính.
Giao điểm của các tia ló hoặc đường kéo dài của các tia ló là ảnh S’ của S.
a) Trường hợp tạo ảnh thật
b) Trường hợp tạo ảnh ảo