Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y’= -2f’(x) nên hàm số nghịch biến trên (-∞;-2),(-1;2) và (4;+∞).
Chọn đáp án B.

Đáp án D
Khẳng định số II sai.
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng - ∞ ; - 2

Đáp án D
Khẳng định số II sai. Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( − ∞ ; − 2 )

Đáp án B
Ta có: D = - 2 ; + ∞ và y ' = 1 x + 2 - 3 x + 2 2 = x - 1 x + 2 2 > 0 ⇔ x > 1
Do đó hàm số đã cho đồng biến trên khoảng 1 ; + ∞ .

Đáp án D
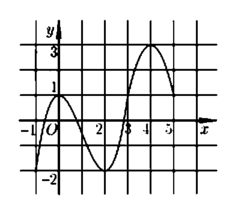
Dựa vào hình vẽ, ta thấy rằng
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.


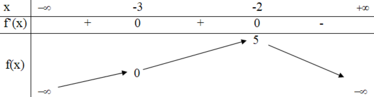
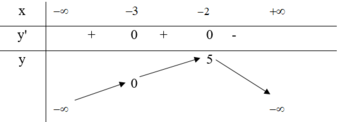
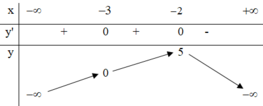
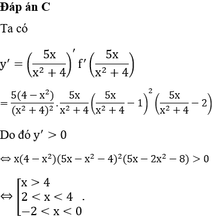
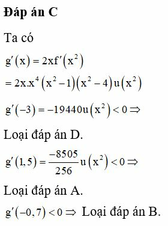
Đáp án B
y ' = 2 x − 4 > 0 ⇔ x > 2 nên hàm số đồng biến trên khoảng 2 ; + ∞