K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
1

5 tháng 10 2015
ta có:
\(y'=\frac{\left(\frac{1-x^2}{1+x^2}\right)'}{\frac{1-x^2}{1+x^2}}=\frac{\frac{-2x.\left(1+x^2\right)-2x.\left(1-x^2\right)}{\left(1+x^2\right)^2}}{\frac{1-x^2}{1+x^2}}=\frac{\frac{-4x}{\left(1+x^2\right)^2}}{\frac{1-x^2}{1+x^2}}=\frac{-4x}{\left(1+x^2\right)\left(1-x^2\right)}=\frac{-4x}{1-x^4}\)

5 tháng 10 2015
ta có:
\(y'=e^xlnx+xe^xlnx+xe^x\frac{1}{x}=e^x\left(lnx+xlnx+1\right)\)

CM
7 tháng 3 2018
B
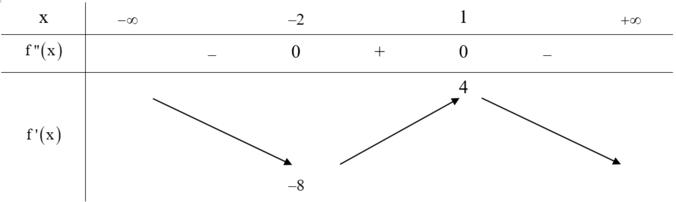
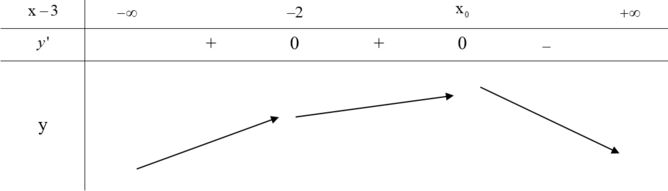
Từ đồ thị của hàm số f"(x) ta có bảng biến
thiên của hàm số f'(x) như sau:

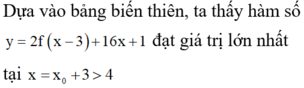

CM
15 tháng 7 2019
Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :
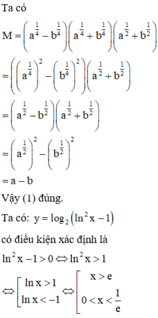
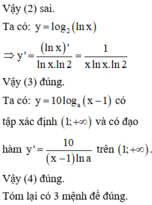

CM
23 tháng 10 2017
Đáp án C
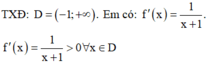
Đồ thị hàm số y = f'(x) không cắt trục hoành
Hay phương trình f'(x) = 0 vô nghiệm

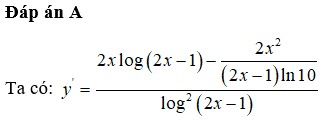



Đáp án A