Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Chọn chiều dương là chiều của v 1 ¯ ( v 1 > 0) ta có:
m 1 v 1 - m 2 v 2 = - m 1 v 1 ' + m 2 v 2 ' → m 1 m 2 = v 2 , + v 2 v 1 , + v 1 = 0 , 6

giải
chọn chiều dương chiều chuyển động xe 1 ban đầu:
\(\text{P 1 − P 2 = − P 1 + P 2 => 0.5.3 − 0 , 25.2 = − 0 , 5.2 + 0 , 25. v 2 ′ => v 2 ′ = 8 m / s P 1 − P 2 = − P 1 + P 2 => 0.5.3 − 0 , 25.2 = − 0 , 5.2 + 0 , 25. v 2 ′ => v 2 ′ = 8 m / s }\text{P}\text{P}1-P2=-P1+P2\Rightarrow0,5.3-0,25.2=-0,5.2+0,25.V2'\Rightarrow V2'=8m/s\)

Chọn chiều dương là chiều chuyển động toa thứ nhất
Áp dụng định luật bảo toàn động lương:
\(mv=m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}\)
\(\Rightarrow mv=m_1v_1-m_2v_2\)
\(\Rightarrow5v=3.6-2.4\) => v = 2 m/s

Chọn chiều + là chiều chuyển động của m1 ban đầu
Bảo toàn động lượng cho hệ (m1+m2) trước và sau va chạm
\(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p_1'}+\overrightarrow{p_2'}\)
\(\rightarrow m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=m_1\overrightarrow{v_1'}+m_2\overrightarrow{v_2'}\)
Vhiếu lên chiều +
\(3,5.5+0=3,5.v_1'+5.3,6\)
\(\rightarrow v_1'=-0,14\left(\frac{m}{s}\right)\)
Toa 1 chuyển động ngược chiều + với
\(v_1'=0,14\left(\frac{m}{s}\right)\)
bài này gồm hai giai đoạn
trước va chạm
p1= m1.v1 + m2..v2=3,5.5+5.3,6=35,5
sau va chạm
p2= m1.v1'+ m2 .v2= 3,5.v1+ 5.3,6=3,5.v1+18
áp dụng định luật bảo toàn động lượng ta có:
m1.v1+m2.v2= m1.v1'+m2.v2
<=> 35,5=3,5v1+18
=> v1=5m/s
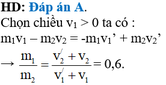




Đáp án A.
Chọn chiều v 1 > 0 ta có :
m 1 v 1 − m 2 v 2 = − m 1 v 1 / + m 2 . v 2 / ⇒ m 1 m 2 = v 2 / + v 2 v 1 / + v 1 = 0 , 6