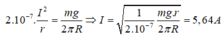Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
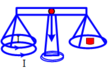
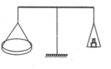
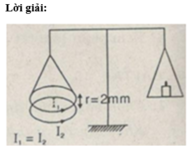
Chu vi của mỗi vòng dây là: I C = 2 π R .
Vì hai vòng dây ở cách nhau một khoảng rất nhỏ nên:
Lực tác dụng lên mỗi vòng dây là:
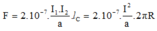
Điều kiện để cân thăng bằng là:
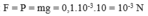
Cường độ dòng điện trong mỗi vòng dây là:
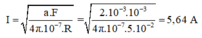

a) Chiều lên phương của sợi dây:
\(T\cos a=P=mg\)
\(T\sin a=F\left(F=kq_1.\frac{q_2}{r^2}\right)\)
Mà hai quả nhiểm điên như nhau.
\(\Rightarrow q_1=q_2=q\Rightarrow F=mg.\tan a\)
a là góc lệch sợi dây phương ngang.
Có: \(\sin a=\frac{r}{\left(2l\right)}\)
Vì a rất nhỏ \(\Rightarrow\sin a=\tan a=\frac{3}{50}\)
Thay vào ra \(F=3,6.10^{-4}\Rightarrow q=1,2.10^{-8}C\)
b) Lúc này: \(F=\frac{k.q^2}{e.r^2}\)
Với e là hằng số điện mới.
\(\Rightarrow F=\frac{mg.q^2}{er^2}=mg.\tan a=mg.\sin a=\frac{mg.r'}{2l'}\)
Thay vào tính được r' = 20 cm

Gọi q1,q2 là điện tích của quả cầu 1 và quả cầu 2 trước khi chúng tiếp xúc với nhau.Độ lớn của lực tương tác giữa chúng được xác định theo định luật Culông :
\(F_1=k\frac{\left|q_1q_2\right|}{r^2}\) từ đó \(q_1q_2=-\frac{F_1r^2}{k}\) (có dấu \(\text{"−"}\) vì hai điên tích \(q_1,q_2\) trái dấu)
Thay số ta được : \(q_1q_2=-\frac{6,4}{9}.10^{-13}\left(1\right)\)
Sau khi tiếp xúc với nhau, điện tích của hai quả cầu trở nên bằng nhau và có độ lớn bằng \(\frac{\left|q_1+q_2\right|}{2}\) do đó lực đẩy giữa chúng là: \(F_2=\frac{k\left(\frac{q_1+q_2}{2}\right)^2}{r^2}\)
Suy ra \(\left(q_1+q_2\right)^2=\frac{4F_2r^2}{k}\) Thay số vào ta được \(\left(q_1+q_2\right)^2=16.10^{-14}\)
hay : \(q_1+q_2=\pm4.10^{-7}\left(2\right)\)
Giải hệ phương trình (1),(2) ta được :
\(q_1=-\frac{4}{3}.10^{-7}\approx-1,33.10^{-7}C\)
\(q_2=\frac{16}{3}.10^{-7}\approx5,33.10^{-7}C\)
hoặc \(q_1=\frac{4}{3}.10^{-7}\approx1,33.10^{-7}C\)
\(q_2=-\frac{16}{3}.10^{-7}\approx-5,33.10^{-7}C\)