Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựa vào đk 2 điện tích đẩy nhau và tổng điện tích của chúng dương. ta có thể biết ngay 2 vật mang điện tích dương
ta có \(F=\dfrac{k\times|q_1q_2|}{r^2}\Leftrightarrow q_1q_2=2\times10^{-10}\) (1)
theo bài có \(q_1+q_2=3\times10^{-5}\) (2)
từ \(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}q_1=3\times10^{-5}-q_2\\\left(3\times10^{-5}-q_2\right)\times q_2=2\times10^{-10}\left(3\right)\end{matrix}\right.\)
giải (3) \(\Rightarrow\left[{}\begin{matrix}q_2=2\times10^{-5}\left(c\right)\Rightarrow q_1=10^{-5}\left(c\right)\\q_2=10^{-5}\left(c\right)\Rightarrow q_1=2\times10^{-5}\left(c\right)\end{matrix}\right.\)
KL có 2 TH nghiệm

Ta có F = k q 1 q 2 ε r 2 → q 1 q 2 = ε r 2 F k → q 1 q 2 = 1 , 8 9.10 9 = 2.10 10
Do hai điện tích đẩy nhau nên chúng cùng dấu, tức là
q 1 q 2 > 0 → q 1 q 2 = 2.10 − 5 q 1 + q 2 = 3.10 − 5
Áp dụng định lí Viet, ta có q 1 v à q 2 là nghiệm của phương trình bậc 2: q 2 − S q + P = 0
Hay q 2 − 3.10 − 5 q + 2.10 − 5 = 0 → q 1 = 10 − 5 C q 2 = 2.10 − 5 C
hoặc q 1 = 2.10 − 5 C q 2 = 10 − 5 C

1.2/
\(F=\dfrac{k\left|q_1q_2\right|}{r^2}=\dfrac{kq^2}{r^2}\Leftrightarrow\dfrac{9.10^9.q^2}{0,04^2}=10^{-5}\Rightarrow q\approx1,33.10^{-9}\left(C\right)\)
\(r'^2=\dfrac{9.10^9.\left(1,33.10^{-9}\right)^2}{2,5.10^{-6}}=...\Rightarrow r=...\left(m\right)\)
2.2/ \(F=\dfrac{k\left|q_1q_2\right|}{r^2}\Leftrightarrow\left|q_1q_2\right|=\dfrac{1,8.1^2}{9.10^9}=...\)
Đẩy nhau=> 2 điện tích cùng dấu \(\Rightarrow q_1q_2=\dfrac{1,8}{9.10^9}\Leftrightarrow q_2=\dfrac{1,8}{9.10^9.q_1}\)
\(\Rightarrow\left\{{}\begin{matrix}q_1+q_2=3.10^{-5}\\q_2=\dfrac{1,8}{9.10^9.q_1}\end{matrix}\right.\Rightarrow...\)
P/s: Số xấu lắm, với cả tui hiện ko có cầm máy tính nên bạn tự tính nốt nhó :)

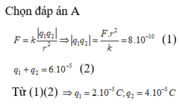
Vì hai quả cầu đẩy nhau nên chúng có điện tích cùng dấu, do đó ta có:
F = k q 1 q 2 ε r 2 → q 1 q 2 = ε r 2 F k = 1 , 8 9.10 9 = 0 , 2.10 − 9 = P
Mặt khác → q 1 + q 2 = 3.10 − 5 = S → q 1 q 2 = 0 , 2.10 9 = P q 1 + q 2 = 3.10 − 5 = S
Theo định lí Vi-ét:
q 2 − S q + P = 0 → q 2 − 3.10 − 5 q + 0 , 2.10 − 9 = 0 → q 1 = 2.10 − 5 C q 2 = 10 − 5 C