Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) ĐK: \(x\ge\frac{3}{2}\)
pt \(\Leftrightarrow\frac{2x-2-\left(6x-9\right)}{\sqrt{2x-2}+\sqrt{6x-9}}=16x^2-28x-20x+35\)
\(\Leftrightarrow\frac{-4x+7}{\sqrt{2x-2}+\sqrt{6x-9}}=4x\left(4x-7\right)-5\left(4x-7\right)\)
\(\Leftrightarrow-\frac{4x-7}{\sqrt{2x-2}+\sqrt{6x-9}}=\left(4x-7\right)\left(4x-5\right)\)
\(\Leftrightarrow\left(4x-7\right)\left(\frac{1}{\sqrt{2x-2}+\sqrt{6x-9}}+4x-5\right)=0\)
\(\Leftrightarrow4x-7=0\Leftrightarrow x=\frac{7}{4}\) (nhận)
2) ĐK: \(2\le x\le4\)
pt \(\Leftrightarrow\sqrt{x-2}+\sqrt{a-x}=2\left(x^2-6x+9\right)+7x-19\)
\(\Leftrightarrow\sqrt{x-2}-\left(7x-20\right)+\sqrt{4-x}-1=2\left(x-3\right)^2\)
\(\Leftrightarrow\frac{x-2-\left(7x-20\right)^2}{\sqrt{x-2}+7x-20}+\frac{4-x-1}{\sqrt{4-x}+1}=2\left(x-3\right)^2\)
\(\Leftrightarrow\frac{\left(x-3\right)\left(134-49x\right)}{\sqrt{x-2}+\left(7x-20\right)}+\frac{3-x}{\sqrt{4-x}+1}=2\left(x-3\right)^2\)
\(\Leftrightarrow x-3=0\Leftrightarrow x=3\) (nhận)

1. con người
2. bác tài bỏ lại xe đó và đi qua cầu
3. vì chúng bò theo đường thẳng nằm ngang
4.tôi sẽ bị treo cổ
5. đập con ma xanh trước, con ma đỏ thấy thế sợ quá mặt mày chuyển sang màu xanh, đập thêm phát nữa là chết cả 2 con.
6. con cua xanh vì cua đỏ đã được luộc chín rồi.


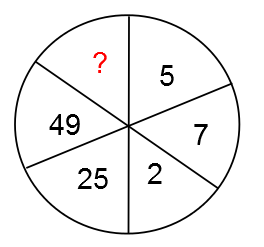
Theo đề bài ta nhận thấy số đối diện số 5 là số 25
=> Quy luật là : n2
=> 52 = 25
=> 72 = 49
<=> 22 = 4

\(\frac{2x+7}{4}=\frac{3-5y}{7}=\frac{2x-5y}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{2x+7}{4}=\frac{3-5y}{7}=\frac{2x-5y}{9}=\frac{\left(2x+7\right)+\left(3-5y\right)-\left(2x-5y\right)}{4+7-9}\)
\(=\frac{2x+7+3-5y-2x+5y}{2}=\frac{10}{2}=5\)
Suy ra:\(\frac{2x+7}{4}=5\Rightarrow2x+7=20\Rightarrow x=\frac{13}{2}\)
\(\frac{3-5y}{7}=5\Rightarrow3-5y=35\Rightarrow x=-\frac{32}{5}\)

A B C c b a I
Ta có : \(a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=0\Leftrightarrow a.\overrightarrow{IA}+\left(b+c\right).\overrightarrow{IA'}=\overrightarrow{0}\) (Công thức thu gọn)
\(\Rightarrow I\in AA'\) và
\(\frac{IA}{IA'}=\frac{b+c}{a}=\frac{c}{\frac{ac}{b+c}}=\frac{BA}{BA'}\)
Nhờ vào tính chất đường phân giác, dễ dàng thấy điểm I thuộc tia phân giác góc B, tức I là tâm của đường tròn ngoại tiếp tam giác ABC
=> Điều đó đúng với giả thiết.
Vậy ta có đpcm

Gọi đàn thiên nga là x , ta có :
x + \(\frac{1}{2}\) x + 2 = 200
x + \(\frac{1}{2}\) x = 200 - 2 = 198
x . ( 1 + \(\frac{1}{2}\) ) = 198
x . \(\frac{3}{2}\) = 198
x = 198 : \(\frac{3}{2}\)
x = 132
Vậy đàn thiên nga có 132 con
Chúng tôi thêm 12 chúng tôi
????????