Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện: 2 ≤ n ∈ N
Ta có
A n + 3 3 - 6 C n + 1 3 = 294 ⇔ n + 3 ! n ! - 6 n + 1 ! 3 ! n - 2 ! = 294 ⇔ n + 3 n + 2 n + 1 - n + 1 n n - 1 = 294 ⇔ n 2 + 2 n - 48 = 0 ⇔ n = 6 n = - 8
So với điều kiện chọn n = 6
Với n = 6 ta có 2 x 4 y + y 2 x 2 6 = ∑ k = 0 6 C 0 k 2 x 4 y 6 - k y 2 x 2 k = ∑ k = 0 6 C 0 k 2 6 - k x 24 - 6 k y - 6 + 3 k
Giả thiết bài toán cho ta 24 - 6 k - 6 + 3 k = 18 ⇔ k - 3 2 = 0 ⇔ k = 3
Khi k = 3 ta thu được số hạng thỏa mãn yêu cầu bài toán là: C 6 3 2 2 x 6 y 3 = 160 x 6 y 3
Đáp án D

Ta có x + 1 x n = ∑ k = 0 n C n k x n - 2 k
Theo đề ta có C n 0 + C n 1 = 24 ⇔ 1 + n = 24 ⇔ n = 23
Số hạng chứa x mũ nguyên dương thỏa n - 2 k > 0 ⇔ k < n 2 = 23 2
Do k ∈ Z nên k ∈ 1 ; 2 ; 3 ; . . 11 .
Suy ra có 12 số hạng chứa x mũ nguyên dương
Đáp án C

Đáp án A
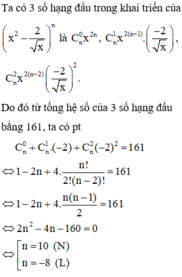
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
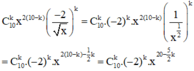
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho
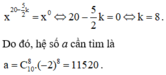
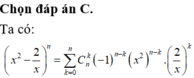
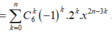
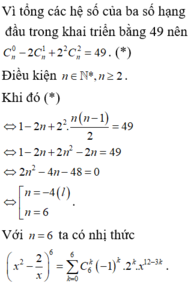



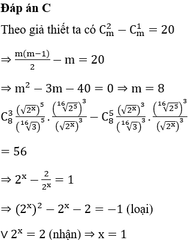
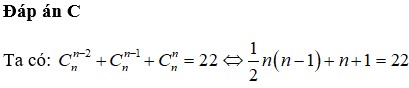
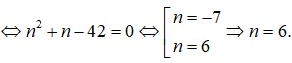
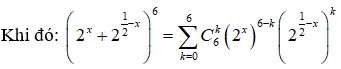
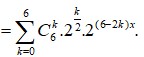
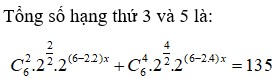
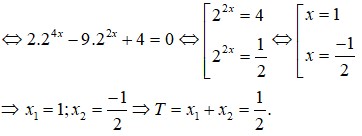

Ta có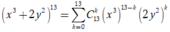
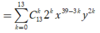
Từ giả thiết bài toán, ta có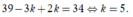
Vậy hệ số của T k bằng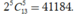
Chọn C.