
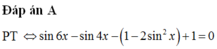
![]()
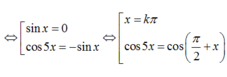
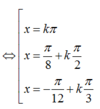
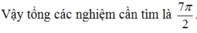
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
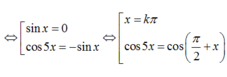
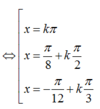
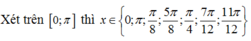
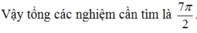

điều kiện : cosx\(\ne\)\(\frac{1}{\sqrt{2}}\)=> x\(\ne\)\(\pm\)\(\frac{\pi}{4}\)+2k\(\pi\), k\(\in\)Z
pt<=> tử số =0
<=>cos2x-sin(3x-\(\frac{\pi}{4}\)+x+\(\frac{3\pi}{4}\))-sin(3x-\(\frac{\pi}{4}\)-x-\(\frac{3\pi}{4}\))-2=0
<=> cos2x-sin(x+\(\frac{\pi}{2}\))-sin(2x-\(\pi\))-2=0
<=> cos2x-cosx+sin2x-2sin2x-2cos2x=0
<=>-cos2x-coxs+2sinx.cosx-2sin2x=0
đến đây bạn nhóm lại ra nghiệm rồi kiểm tra đk là xong

phương trình tương đương:
sin2x+cos2x+\(\sqrt{2}\)sin(x+\(\frac{\pi}{4}\))+2sinx.cosx+cos2x-sin2x=0
<=> 2cos2x+2sinx.cosx+\(\sqrt{2}\)sin(x+\(\frac{\pi}{4}\))=0
<=> 2cosx(sinx+cosx)+\(\sqrt{2}\)sin(x+\(\frac{\pi}{4}\))=0
<=>(2cosx+1).\(\sqrt{2}\)sin(x+\(\frac{\pi}{4}\))=0
<=>\(\left[\begin{array}{nghiempt}sin\left(x+\frac{\pi}{4}\right)=0\\2cosx+1=0\end{array}\right.\)
<=> \(\left[\begin{array}{nghiempt}x=k\pi-\frac{\pi}{4}\\x=\pm\frac{1}{2}+k2\pi\end{array}\right.\)với k\(\in\)Z
pt có 2 nghiệm như trên