K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 1 2018
a) \(\dfrac{x}{3}-\dfrac{2x+1}{2}=\dfrac{x}{6}-x\)
\(\Leftrightarrow\dfrac{2x}{6}-\dfrac{3\left(2x+1\right)}{6}=\dfrac{x}{6}=\dfrac{6x}{6}\)
\(\Leftrightarrow2x-3\left(2x+1\right)=x-6x\)
\(\Leftrightarrow2x-6x-3=x-6x\)
\(\Leftrightarrow2x-6x-x+6x=3\)
\(\Leftrightarrow x=3\)
\(S=\left\{3\right\}\)
b) \(\dfrac{2+x}{5}-0,5x=\dfrac{1-2x}{4}+0,25\)
\(\Leftrightarrow\dfrac{4\left(2+x\right)}{20}-\dfrac{10x}{20}=\dfrac{5\left(1-2x\right)}{20}+\dfrac{5}{20}\)
\(\Leftrightarrow4\left(2+x\right)-10x=5\left(1-2x\right)+5\)
\(\Leftrightarrow8+4x-10x=5-10x+5\)
\(\Leftrightarrow4x-10x+10x=5+5-8\)
\(\Leftrightarrow4x=2\)
\(\Leftrightarrow x=\dfrac{1}{2}\)
\(S=\left\{\dfrac{1}{2}\right\}\)
17 tháng 5 2022
a: \(\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(\dfrac{1}{2}x\right)^2-\left(2x-3\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(\dfrac{1}{2}x-2x+3\right)\left(\dfrac{1}{2}x+2x-3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(3-\dfrac{3}{2}x\right)\left(\dfrac{5}{2}x-3\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{6}{5}\right\}\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{4}{3}\\\left(3x+4\right)^2-\left(2x\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{4}{3}\\\left(5x+4\right)\left(x+4\right)=0\end{matrix}\right.\)
\(\Leftrightarrow x=-\dfrac{4}{5}\)
c: \(\Leftrightarrow\left\{{}\begin{matrix}x>=12\\\left(5x-x+12\right)\left(5x+x-12\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=12\\\left(4x+12\right)\left(6x-12\right)=0\end{matrix}\right.\)
hay \(x\in\varnothing\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{10}{3}\\\left(2,5x-1,5x-5\right)\left(2,5x+1,5x+5\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{10}{3}\\\left(x-5\right)\left(4x+5\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{-\dfrac{5}{4};5\right\}\)
17 tháng 5 2022
a: \(\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left(3x-2-2x\right)\left(3x-2+2x\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left(x-2\right)\left(5x-2\right)=0\end{matrix}\right.\)
hay x=2
b: \(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{10}{3}\\\left(-3,5x-1,5x-5\right)\left(-3,5x+1,5x+5\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{10}{3}\\\left(-5x-5\right)\left(-2x+5\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{-1;\dfrac{5}{2}\right\}\)
c: \(\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{1}{3}\\\left(3x-1-x-15\right)\left(3x-1+x+15\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{1}{3}\\\left(2x-16\right)\left(4x+14\right)=0\end{matrix}\right.\Leftrightarrow x=8\)
d: \(\Leftrightarrow\left|x-2\right|=0,5x-4\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=8\\\left(0,5x-4-x+2\right)\left(0,5x-4+x-2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=8\\\left(-0,5x-2\right)\left(1,5x-6\right)=0\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
CM
3 tháng 1 2019
Ta có: |0,5x| = 0,5x khi 0,5x ≥ 0 ⇔ x ≥ 0
|0,5x| = -0,5x khi 0,5x < 0 ⇔ x < 0
Ta có: 0,5x = 3 – 2x ⇔ 0,5x + 2x = 3 ⇔ 2,5x = 3 ⇔ x = 1,2
Giá trị x = 1,2 thỏa mãn điều kiện x ≥ 0 nên 1,2 là nghiệm của phương trình.
-0,5x = 3 – 2x ⇔ -0,5x + 2x = 3 ⇔ 1,5x = 3 ⇔ x = 2
Giá trị x = 2 không thỏa mãn điều kiện x < 0 nên loại.
Vậy tập nghiệm của phương trình là S = {1,2}
TH
14 tháng 6 2017
a,Với k =0 thì biểu thức bằng:
4x3-25=0 hay 4x3 = 25 nên x=\(\sqrt[3]{\frac{25}{4}}\)
b,Với k =(-3) thì biểu thức bằng:\(4x^3-25+9-12x=0\)
hay :\(4x^3-12x=16\)
\(4x\left(x^2-3\right)=16\)
\(x^2-3=\frac{4}{x}\) nên suy ra \(\left(x^2-3\right):\frac{4}{x}=1\)
hay \(x^3-3x=4\)
nên nếu với x là một số tự nhiên thì phương trình vô nghiệm
PT
1
CM
21 tháng 2 2017
Đáp án: C
-0,5x - 2 = 0 ⇔ -0,5x = 2 ⇔ x =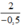 
⇔ x = -4.
Vậy phương trình có nghiệm x = - 4.
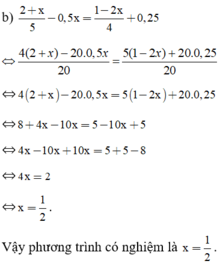
- 0,5x + 2,4 = 0
⇔ -0,5x = -2,4
⇔ x = (-2,4)/(-0.5)
⇔ x = 4,8
Vậy phương trình có một nghiệm duy nhất x = 4,8