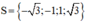K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DA
1
YH
23 tháng 7 2019
a) \(x+\sqrt{4x^2-4x+1}=2\)
\(\Leftrightarrow x+\sqrt{\left(2x-1\right)^2}=2\)
\(\Leftrightarrow x+|2x-1|=2\)
\(TH1:x\ge0\)
\(\Leftrightarrow x+2x-1=2\)
\(\Leftrightarrow3x-1=2\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\left(TM\right)\)
\(TH2:x< 0\)
\(\Leftrightarrow x-2x-1=2\)
\(\Leftrightarrow-x-1=2\)
\(\Leftrightarrow-x=3\)
\(\Leftrightarrow x=-3\left(TM\right)\)
Vậy:...
b) \(3x-1-\sqrt{4x^2-12x+9}=0\)
\(\Leftrightarrow3x-1-\sqrt{\left(2x-3\right)^2}=0\)
\(\Leftrightarrow3x-1-|2x-3|=0\)
\(TH1:x\ge0\)
\(\Leftrightarrow3x-1-2x+3=0\)
\(\Leftrightarrow x+2=0\Leftrightarrow x=-2\left(KTM\right)\)
\(TH2:x< 0\)
\(\Leftrightarrow3x-1+2x-3=0\)
\(\Leftrightarrow5x-4=0\Leftrightarrow x=\frac{4}{5}\left(KTM\right)\)
Vậy: pt vô nghiệm
Học Tốt!!!
YH
18 tháng 8 2019
a)...ghi lại đề...
\(\Leftrightarrow\sqrt{x^2-x-2x+2}=\sqrt{x-1}\)
\(\Leftrightarrow\sqrt{x\left(x-1\right)-2\left(x-1\right)}=\sqrt{x-1}\)
\(\Leftrightarrow\sqrt{\left(x-2\right)\left(x-1\right)}=\sqrt{x-1}\)
\(\Leftrightarrow\sqrt{x-2}\cdot\sqrt{x-1}=\sqrt{x-1}\)
\(\Leftrightarrow\sqrt{x-2}=\frac{\sqrt{x-1}}{\sqrt{x-1}}=1\)
\(\Leftrightarrow\sqrt{x-2}^2=1^2\)
\(\Leftrightarrow x-2=1\)(Vì \(x-2\ge0\Leftrightarrow x\ge2\))
\(\Leftrightarrow x=3\)
\(\)
18 tháng 8 2019
\(a,\sqrt{x^2-3x+2}=\sqrt{x-1}\)
\(\Rightarrow x^2-3x+2=x-1\)
\(\Rightarrow x^2-4x+3=0\)
\(\Rightarrow x^2-x-3x+3=0\)
\(\Rightarrow\left(x-3\right)\left(x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}}\)
Vậy..........
29 tháng 10 2020
a) \(\text{Đ}K\text{X}\text{Đ}:\frac{3}{2}\le x\le\frac{5}{2}\)
Áp dụng BĐT Bunhiacopxki ta có:
\(VT=\sqrt{2x-3}+\sqrt{5-2x}\le\sqrt{2\left(2x-3+5-2x\right)}=2\)
Dấu '=' xảy ra khi \(\sqrt{2x-3}=\sqrt{5-2x}\Leftrightarrow x=2\)
Lại có: \(VP=3x^2-12x+14=3\left(x-2\right)^2+2\ge2\)
Dấu '=' xảy ra khi x=2
Do đó VT=VP khi x=2
29 tháng 10 2020
b) ĐK: \(x\ge0\). Ta thấy x=0 k pk là nghiệm của pt, chia 2 vế cho x ta có:
\(x^2-2x-x\sqrt{x}-2\sqrt{x}+4=0\Leftrightarrow x-2-\sqrt{x}-\frac{2}{\sqrt{x}}+\frac{4}{x}=0\)
\(\Leftrightarrow\left(x+\frac{4}{x}\right)-\left(\sqrt{x}+\frac{2}{\sqrt{x}}\right)-2=0\)
Đặt \(\sqrt{x}+\frac{2}{\sqrt{x}}=t>0\Leftrightarrow t^2=x+4+\frac{4}{x}\Leftrightarrow x+\frac{4}{x}=t^2-4\), thay vào ta có:
\(\left(t^2-4\right)-t-2=0\Leftrightarrow t^2-t-6=0\Leftrightarrow\left(t-3\right)\left(t+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=3\\t=-2\end{cases}}\)
Đối chiếu ĐK của t
\(\Rightarrow t=3\Leftrightarrow\sqrt{x}+\frac{2}{\sqrt{x}}=3\Leftrightarrow x-3\sqrt{x}+2=0\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=1\end{cases}}\)
S
2
MN
2 tháng 4 2019
\(6x^4+25x^3+12x^2-25x+6=0.\)
\(\Leftrightarrow\left(2x^2+x-2\right)\left(3x^2+8x-3\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x+2\right)\left(x+3\right)\left(3x-1\right)=0\)
29 tháng 10 2020
a) \(\sqrt{x^2-6x+9}=3\)
⇔ \(\sqrt{\left(x-3\right)^2}=3\)
⇔ \(\left|x-3\right|=3\)
⇔ \(\orbr{\begin{cases}x-3=3\\x-3=-3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=6\\x=0\end{cases}}\)
b) \(\sqrt{x^2-8x+16}=x+2\)
⇔ \(\sqrt{\left(x-4\right)^2}=x+2\)
⇔ \(\left|x-4\right|=x+2\)
⇔ \(\orbr{\begin{cases}x-4=x+2\left(x\ge4\right)\\4-x=x+2\left(x< 4\right)\end{cases}\Leftrightarrow}x=1\)
c) \(\sqrt{x^2+6x+9}=3x-6\)
⇔ \(\sqrt{\left(x+3\right)^2}=3x-6\)
⇔ \(\left|x-3\right|=3x-6\)
⇔ \(\orbr{\begin{cases}x-3=3x-6\left(x\ge3\right)\\3-x=3x-6\left(x< 3\right)\end{cases}}\Leftrightarrow x=\frac{9}{4}\)
d) \(\sqrt{x^2-4x+4}-2x+5=0\)
⇔ \(\sqrt{\left(x-2\right)^2}-2x+5=0\)
⇔ \(\left|x-2\right|-2x+5=0\)
⇔ \(\orbr{\begin{cases}x-2-2x+5=0\left(x\ge2\right)\\2-x-2x+5=0\left(x< 2\right)\end{cases}}\Leftrightarrow x=3\)
TM
20 tháng 11 2017
(1)Phương trình đã cho tương đương với:
√3x2−7x+3−√3x2−5x−1=√x2−2−√x2−3x+43x2−7x+3−3x2−5x−1=x2−2−x2−3x+4
⇔−2x+4√3x2−7x+3+√3x2−5x−1=3x−6√x2−2+√x2−3x+4⇔−2x+43x2−7x+3+3x2−5x−1=3x−6x2−2+x2−3x+4
⇔(x−2)(3√x2−2+√x2−3x+4+2√3x2−7x+3+√3x2−5x−1)=0⇔(x−2)(3x2−2+x2−3x+4+23x2−7x+3+3x2−5x−1)=0
Đến đây thì bạn có thể suy ra nghiệm của phương trình sau cùng là x=2x=2. Kiểm tra lại điều kiện ban đầu để kết luận nghiệm của phương trình đã cho.
(2)đk:23≤x≤723≤x≤7
Đến đây thì bạn có thể suy ra nghiệm của phương trình sau cùng là x=2x=2. Kiểm tra lại điều kiện ban đầu để kết luận nghiệm của phương trình đã cho.
(2)đk:23≤x≤723≤x≤7
Phương trình đã cho tương đương với:
3x−18√3x−2+4+x−6√7−x−1+(x−6)(3x2+x−2)3x−183x−2+4+x−67−x−1+(x−6)(3x2+x−2)=0
⇔(x−6)(3√3x−2+4+1√7−x−1+3x2+x−2)⇔(x−6)(33x−2+4+17−x−1+3x2+x−2)=0
⇔x=6⇔x=6
vì với 23≤x≤723≤x≤7
thì: (3√3x−2+4+1√7−x−1+3x2+x−2)(33x−2+4+17−x−1+3x2+x−2)>0
Cả ba phương trình trên đều là phương trình trùng phương.
3x4 – 12x2 + 9 = 0 (1)
Đặt x2 = t, t ≥ 0.
(1) trở thành: 3t2 – 12t + 9 = 0 (2)
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1 và t2 = 3.
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x2 = 3 ⇒ x = ±√3.
+ t = 1 ⇒ x2 = 1 ⇒ x = ±1.
Vậy phương trình có tập nghiệm