Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{27}{3\sqrt{3x-2}+6}+\frac{8+4x-x^2}{x\sqrt{6-x}+4}\ge\frac{3}{2}+\frac{2x-14}{3\sqrt{6-x}+2}>0\)
Nên phần còn lại vô nghiệm

Lấy pt 2 trừ 2 lần pt 1:
\(3x^2-4y^3=3y^3-4x^2+7\Leftrightarrow y^3=x^2-1\)
Lấy pt 2 trừ 2 lần pt 3:
\(x^2-2y^2-4xy=3y^3+2z^2+7-4xz-4yz-4\)
\(\Leftrightarrow x^2-2y^2-4xy=3\left(x^2-1\right)+2z^2+7-4xz-4yz-4\)
\(\Leftrightarrow x^2+y^2+z^2+2xy-2yz-2zx=0\)
\(\Leftrightarrow\left(x+y-z\right)^2=0\)
\(\Leftrightarrow x+y=z\)
Hy vọng nó giúp được bạn

\(\begin{cases}x^2\left(x-3\right)-y\sqrt{y-3}=-2\left(1\right)\\3\sqrt{x-2}=\sqrt{y\left(y+8\right)}\left(2\right)\end{cases}\) Điều kiện \(x\ge2;y\ge0\) (*)
Khi đó (1) \(\Leftrightarrow x^3-3x^2+2=y\sqrt{y+3}\)
\(\Leftrightarrow\left(x-1\right)^3-3\left(x-1\right)=\left(\sqrt{y+3}\right)^3-3\sqrt{y+3}\left(3\right)\)
Xét hàm số \(f\left(t\right)=t^3-3t\) trên \(\left(1;+\infty\right)\)
Ta có \(f\left(t\right)=3t^2-3=3\left(t^2-1\right)\ge0\) với mọi \(t\ge1\) suy ra hàm số đồng biến trên \(\left(1;+\infty\right)\)
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với (3) rồi trừ đi phương trình (3) ta được:
Giải hệ phương trình trên ta được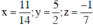
Vậy hệ phương trình có nghiệm