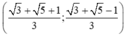PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VN
17 tháng 4 2017
Nhận cả 2 về với cần 5 con PT kia thì nhắn với (1+căn 3) rồi công đại số sẽ khu y
HH
1 tháng 10 2020
\(1)\hept{\begin{cases}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\left(1\right)\\\left(1-\sqrt{3}\right)x+y\sqrt{5}=1\left(2\right)\end{cases}}\)
Từ (1) ta rút ra được : \(x=\frac{1+\left(1+\sqrt{3}\right)y}{\sqrt{5}}\left(3\right)\)
Thay (3) vào phương trinh (2) ta được :
\(\frac{1+\left(1+\sqrt{3}\right)y}{\sqrt{5}}.\left(1-\sqrt{3}\right)+y\sqrt{5}=1\)
\(\Leftrightarrow\frac{1-\sqrt{3}+\left(1+\sqrt{3}\right)\left(1-\sqrt{3}\right)y+5y}{\sqrt{5}}=1\)
\(\Leftrightarrow1-\sqrt{3}-2y+5y=\sqrt{5}\)
\(\Leftrightarrow3y=\sqrt{3}+\sqrt{5}-1\)
\(\Leftrightarrow y=\frac{\sqrt{3}+\sqrt{5}-1}{3}\)vào (3) ta được :
\(x=\frac{1}{\sqrt{5}}.\left[1+\left(1+\frac{1}{\sqrt{3}}\right).\frac{\sqrt{3}+\sqrt{5}-1}{3}\right]\)
\(x=\frac{\sqrt{3}+\sqrt{5}+1}{3}\)
Vậy hệ phương trình có nghiệm \(\left(\frac{\sqrt{3}+\sqrt{5}+1}{3};\frac{\sqrt{3}+\sqrt{5}-1}{3}\right)\)
1 tháng 11 2016
Ta có
x + x2 + x3 + x4 = y + y2 + y3 + y4
<=> (x - y) + (x2 - y2) + (x3 - y2) + (x4 - y4) = 0
<=> (x - y)[1 + x + y + x2 + xy + y2 + (x2 + y2)(x + y)]
<=> (x - y)(2 + 2x + 2y + xy)
\(\Leftrightarrow\orbr{\begin{cases}x-y=0\\2+2x+2y+xy=0\end{cases}}\)
Tới đây bạn tự giải tiếp nhé. Tính không giải đâu mà thấy bạn nhờ nên mới giải tiếp
1 tháng 11 2016
1/ \(\hept{\begin{cases}x+y+xy=5\\\left(x+1\right)^5+\left(y+1\right)^5=35\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=6\\\left(x+1\right)^5+\left(y+1\right)^5=35\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\end{cases}}\)thì hệ thành
\(\hept{\begin{cases}ab=6\\a^5+B^5=35\end{cases}}\)
\(\Rightarrow a^5+\frac{6^5}{a^5}=35\)
PT này vô nghiệm vậy pt ban đầu vô nghiệm
PQ
0
VT
2 tháng 11 2017
câu này quen ha
cái này giả sử x+1>=y-5, rồi cho chúng = nhau
hoặc liên hợp cũng được (PT1)
TH
2
TH
20 tháng 8 2017
<=>\(\hept{\begin{cases}x^3+y^3=1\\x^2\left(x^3-1\right)+y^2\left(y^3-1\right)=0\end{cases}}\)
<=>\(\hept{\begin{cases}x^3+y^3=1\\x^2y^3+x^3y^2=0\end{cases}}\)
Đặt S=x+y;P=xy
khi đó: \(\hept{\begin{cases}S^3-3SP=1\\P^2S=0\end{cases}}\)
sau đó giải hệ pt . kết wa là (0;1);(1:0)
TN
31 tháng 10 2016
Bài 1:
Đặt \(\hept{\begin{cases}S=x+y\\P=xy\end{cases}}\) hpt thành:
\(\hept{\begin{cases}S^2-P=3\\S+P=9\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}S^2-P=3\\S=9-P\end{cases}}\Leftrightarrow\left(9-P\right)^2-P=3\)
\(\Leftrightarrow\orbr{\begin{cases}P=6\Rightarrow S=3\\P=13\Rightarrow S=-4\end{cases}}\).Thay 2 trường hợp S và P vào ta tìm dc
\(\hept{\begin{cases}x=3\\y=0\end{cases}}\)và\(\hept{\begin{cases}x=0\\y=3\end{cases}}\)
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 11 2016
Câu 3: ĐK: \(x\ge0\)
Ta thấy \(x-\sqrt{x-1}=0\Rightarrow x=\sqrt{x-1}\Rightarrow x^2-x+1=0\) (Vô lý), vì thế \(x-\sqrt{x-1}\ne0.\)
Khi đó \(pt\Leftrightarrow\frac{3\left[x^2-\left(x-1\right)\right]}{x+\sqrt{x-1}}=x+\sqrt{x-1}\Rightarrow3\left(x-\sqrt{x-1}\right)=x+\sqrt{x-1}\)
\(\Rightarrow2x-4\sqrt{x-1}=0\)
Đặt \(\sqrt{x-1}=t\Rightarrow x=t^2+1\Rightarrow2\left(t^2+1\right)-4t=0\Rightarrow t=1\Rightarrow x=2\left(tm\right)\)
NB
29 tháng 11 2017
cậu cứ nhân 5 vào phương trình (2)
cộng 2 phương trình lại cậu sẽ ra được x+y-1=2
thế cái vừa tìm được vào 1 trong 2 phương trình thi sẽ ra thêm một phương trình 2x-y=-13
giải hệ rồi tìm được x và y
Từ (1) rút ra được: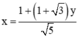
(*)
Thay (*) vào phương trình (2) ta được:
Thay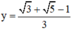
vào (*) ta được:
Vậy hệ phương trình có nghiệm