
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

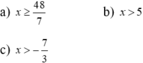

a: (x-3)(x-2)<0
=>x-2>0 và x-3<0
=>2<x<3
b: \(\left(x+3\right)\left(x+4\right)\left(x^2+2\right)\ge0\)
\(\Leftrightarrow\left(x+3\right)\left(x+4\right)\ge0\)
=>x>=-3 hoặc x<=-4
c: \(\dfrac{x-1}{x-2}\ge0\)
nên \(\left[{}\begin{matrix}x-2>0\\x-1\le0\end{matrix}\right.\Leftrightarrow x\in(-\infty;1]\cup\left(2;+\infty\right)\)
d: \(\dfrac{x+3}{2-x}\ge0\)
\(\Leftrightarrow\dfrac{x+3}{x-2}\le0\)
hay \(x\in[-3;2)\)

a, x+2/5 >=0 <=> x+2 >=0 <=> x>=-2
b. x+2/x-3 <0 <=> 1+5/x-3 <0 <=> 5/x-3 <-1 <=> x-3> -5 <=> x>-2
c. x-1/x-3 >1 <=> 1+ 2/x-3 >1 <=> 2/x-3 >0 <=> x-3 >0 <=> x>3

a) \(\frac{x^2+2}{5}\ge0\)
\(\Rightarrow x^2+2\ge0\)( đúng với mọi x )
Vậy \(S=\left\{ℝ\right\}\)
b) \(\frac{x+2}{x-3}< 0\)( ĐKXĐ : \(x\ne3\))
Xét hai trường hợp :
1. \(\hept{\begin{cases}x+2< 0\\x-3>0\end{cases}}\Rightarrow\hept{\begin{cases}x< -2\\x>3\end{cases}}\)( loại )
2. \(\hept{\begin{cases}x+2>0\\x-3< 0\end{cases}}\Rightarrow\hept{\begin{cases}x>-2\\x< 3\end{cases}\Rightarrow}-2< x< 3\)
Vậy nghiệm của bất phương trình là -2 < x < 3
c) \(\frac{x-1}{x-3}>1\)( ĐKXĐ : \(x\ne3\))
\(\Leftrightarrow\frac{x-3+2}{x-3}>1\)
\(\Leftrightarrow1+\frac{2}{x-3}>1\)
\(\Leftrightarrow\frac{2}{x-3}>0\)
\(\Leftrightarrow x-3>0\)
\(\Leftrightarrow x>3\)
Vậy nghiệm của bất phương trình là x > 3
Nhờ bạn khác vẽ trục số nhé vì mình mới lên lớp 8

a) đặt \(\left(x^2+x\right)\)là \(y\)
ta có: \(3y^2-7y+4\)\(=0\)
<=>\(\left(3y-4\right)\left(y-1\right)=0\)
còn lại bạn tự xử nhé

a, ĐKXĐ \(\hept{\begin{cases}x\ne1\\x\ne2\\x\ne3\end{cases}x\ne4}\)
ta có \(đề\Leftrightarrow\frac{\left(x-1\right)^2+1}{x-1}+\frac{\left(x-4\right)^2+4}{x-4}=\frac{\left(x-2\right)^2+2}{x-2}+\frac{\left(x-3\right)^2+3}{x-3}\)
\(\Leftrightarrow x-1+\frac{1}{x-1}+x-4+\frac{4}{x-4}=x-2+\frac{2}{x-2}+x-3+\frac{3}{x-3}\)
\(\Leftrightarrow\frac{1}{x-1}+\frac{4}{x-4}=\frac{2}{x-2}+\frac{3}{x-3}\)
\(\Leftrightarrow\frac{1}{x-1}-\frac{2}{x-2}=\frac{3}{x-3}-\frac{4}{x-4}\)
\(\Leftrightarrow\frac{x-2-2x+2}{\left(x-1\right)\left(x-2\right)}=\frac{3x-12-4x+12}{\left(x-3\right)\left(x-4\right)}\)
\(\Leftrightarrow\frac{-x}{\left(x-1\right)\left(x-2\right)}=\frac{-x}{\left(x-3\right)\left(x-4\right)}\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)=\left(x-3\right)\left(x-4\right)\)(đến đây bạn nhân ra tự giải nhé )
p/s :mình nghĩ bạn viết sai đề đấu + ở phép đầu tiên ko phải - bạn xem lại nhé
b,\(\Leftrightarrow[2\left(x-3\right)]^2-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(2x-6+x-1\right)\left(2x-6-x+1\right)=0\)
\(\Leftrightarrow\left(3x-7\right)\left(x-5\right)=0\)(bạn tự giải)
c,\(\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow x+1=0\Leftrightarrow x=-1\left(do\left(x^2+1>0\right)\right)\)

Nhìn sơ qua thì thấy bài 3, b thay -2 vào x rồi giải bình thường tìm m
Bài 2:
a) \(x+x^2=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\x+1=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\x=0-1\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\x=-1\end{cases}}\)
b) \(0x-3=0\)
\(\Leftrightarrow0x=3\)
\(\Rightarrow vonghiem\)
c) \(3y=0\)
\(\Leftrightarrow y=0\)

a) Ta có: x4 - x3 + 2x2 - x + 1 = 0
=> (x4 + 2x2 + 1) - x(x2 + 1) = 0
=> (x2 + 1)2 - x(x2 + 1) = 0
=> (x2 + 1)(x2 - x + 1) = 0
=> (x2 + 1)[(x2 - x + 1/4) + 3/4] = 0
=> (x2+ 1 )[(x - 1/2)2 + 3/4] = 0
=> pt vô nghiệm (vì x2 + 1 > 0; (x - 1/2)2 + 3/4 > 0)
b) Ta có: x3 + 2x2 - 7x + 4 = 0
=> (x3 - x) + (2x2 - 6x + 4) = 0
=> x(x2 - 1) + 2(x2 - 3x + 2) = 0
=> x(x - 1)(x + 1) + 2(x2 - 2x - x + 2) = 0
=> x(x - 1)(x + 1) + 2(x - 2)(x - 1) = 0
=> (x - 1)(x2 + x + 2x - 4) = 0
=> (x - 1)(x2 + 3x - 4) = 0
=> (x - 1)(x2 + 4x - x - 4) = 0
=> (x - 1)(x + 4)(x - 1) = 0
=> (x - 1)2(x + 4) = 0
=> \(\orbr{\begin{cases}x-1=0\\x+4=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=1\\x=-4\end{cases}}\)
a) \(x^4-x^3+2x^2-x+1=0\)
\(\Leftrightarrow\left(x^4+2x^2+1\right)-x\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)^2-x\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(x^2+1-x\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)\left[\left(x^2-x+\frac{1}{4}\right)+\frac{3}{4}\right]=0\)
\(\Leftrightarrow\left(x^2+1\right)\left[\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\right]=0\)
Ta có: \(\hept{\begin{cases}x^2+1>0\forall x\\\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\forall x\end{cases}}\)
\(\Rightarrow\)Phương trình vô nghiệm
Vậy không có giá trị x thỏa mãn đề bài
b) \(x^3+2x^2-7x+4=0\)
\(\Leftrightarrow\left(x^3-x\right)+\left(2x^2-6x+4\right)=0\)
\(\Leftrightarrow x\left(x^2-1\right)+2\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)+2\left(x^2-x-2x+2\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)+2\left[x\left(x-1\right)-2\left(x-1\right)\right]=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)+2\left(x-2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x\left(x+1\right)+2\left(x-2\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2+x+2x-4\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2+3x-4\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2+4x-x-4\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[x\left(x+4\right)-\left(x+4\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-1\right)^2=0\\x+4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x-1=0\\x+4=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=1\\x=-4\end{cases}}}\)
Vậy x=1; x=-4