Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

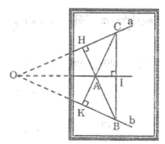
- Kẻ AH ⊥ a kéo dài HA cắt b tại B
- Kẻ AK ⊥ b kéo dài KA cắt a tại C
- Nối BC
- Kẻ AI ⊥ BC, đường thẳng AI đi qua O
Chứng minh:
Vì tam giác OBC có hai đường cao BH và CK cắt nhau tại A nên A là trực tâm của tam giác OBC.
Khi đó OA là đường cao thứ ba nên OA ⊥ BC.
Lại có: AI ⊥ BC nên đường thẳng OA và đường thẳng AI trùng nhau ( vì qua 1 điểm nằm ngoài 1 đường thẳng ta vẽ được một và chỉ một đường thẳng vuông góc với đường thẳng cho trước).
Suy ra: đường thẳng AI đi qua O.

- Kẻ AH⊥aAH⊥a kéo dài, HA cắt b tại B.
- Kẻ AK⊥bAK⊥b kéo dài KA cắt a tại C.
- Kẻ AI⊥BCAI⊥BC, đường thẳng AI đi qua O.
Vì trong ∆OBC có 2 đường cao BH và CK cắt nhau tại A nên A là trực tâm của ∆OBC.
OA là đường cao thứ 3 nên OA⊥BCOA⊥BC
AI⊥BCAI⊥BC nên đường thẳng OA và đường thẳng AI trùng nhau hay đường thẳng AI đi qua O.

-Dùng thước thửng vẽ đg thẳng d
-Lấy điểm O ngoài đg thẳng d
-Đặt eke sao cho 1 cạch của eke trùng với đg thẳng d, cạnh còn lại chứa điểm d
- Vẽ đg thẳng d' chứa điểm O đi qua cạnh của eke
mk có cách dựng đường vuông góc chính xác hơn nhiều mà chỉ dùng thước và compa

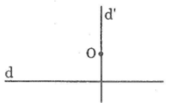
- Đặt êke sao cho một cạnh góc vuông trùng với đường thẳng d.
- Trượt thước theo đường thẳng d đến khi cạnh còn lại đi qua điểm O.
- Kẻ đường thẳng đi qua cạnh góc vuông thứ hai ta được đường thẳng đi qua O và vuông góc với d
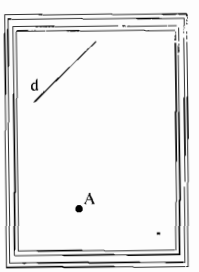
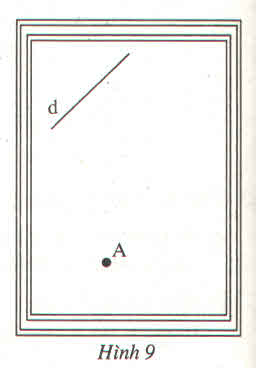


Lấy điểm B ∈d tuỳ ý, dùng eke vẽ đường thẳng c vuông góc với d tại B
Vẽ đường thẳng d’ đi qua A và d’//c
Ta có: d’ ⊥ d.