Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hệ (I): 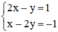
Ta biểu diễn hai đường thẳng (d): 2x – y = 1 và (d’): x – 2y = -1 trên mặt phẳng tọa độ.
+ Xét đường thẳng (d): 2x – y = 1 hay (d) : y = 2x – 1
Chọn x = 0 ⇒ y = -1.
Chọn y = 0 ⇒ x = 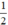
⇒ (d) đi qua hai điểm (0; -1) và 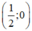
+ Xét (d’) : x – 2y = -1 hay (d’): 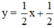
Chọn x = 0 ⇒ y = 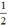
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm 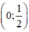 và (-1; 0).
và (-1; 0).
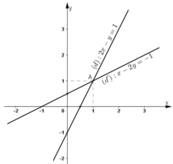
Dựa vào đồ thị thấy hai đường thẳng (d) và (d’) cắt nhau tại A (1; 1).
Thử lại, thay x =1, y=1 vào các phương trình của hệ (I) ta được:
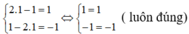
Vậy hệ phương trình (I) có một nghiệm là (1; 1)
b) Xét (II): 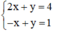
Ta biểu diễn hai đường thẳng (d): 2x + y = 4 và (d’): -x + y = 1 trên mặt phẳng tọa độ.
+ Xét (d): 2x + y = 4 hay (d): y = -2x + 4
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
+ Xét (d’) : -x + y = 1 hay (d’) : y = x + 1.
Chọn x = 0 ⇒ y = 1
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm (0; 1) và (-1; 0).
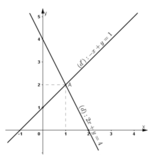
Nhận thấy (d) và (d’) cắt nhau tại A (1; 2).
Thử lại , thay x =1, y=2 vào các phương trình của hệ (II) ta được:
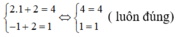
Vậy hệ phương trình (II) có đúng một nghiệm là (1; 2).

Xét hệ (I): 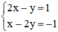
Ta biểu diễn hai đường thẳng (d): 2x – y = 1 và (d’): x – 2y = -1 trên mặt phẳng tọa độ.
+ Xét đường thẳng (d): 2x – y = 1 hay (d) : y = 2x – 1
Chọn x = 0 ⇒ y = -1.
Chọn y = 0 ⇒ x = 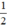
⇒ (d) đi qua hai điểm (0; -1) và 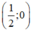
+ Xét (d’) : x – 2y = -1 hay (d’): 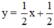
Chọn x = 0 ⇒ y = 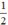
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm 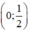 và (-1; 0).
và (-1; 0).
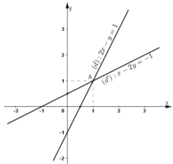
Dựa vào đồ thị thấy hai đường thẳng (d) và (d’) cắt nhau tại A (1; 1).
Thử lại, thay x =1, y=1 vào các phương trình của hệ (I) ta được:
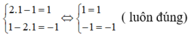
Vậy hệ phương trình (I) có một nghiệm là (1; 1)

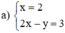
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
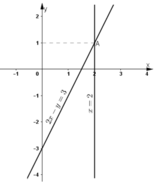
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
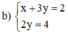
Đường thẳng (d): x + 3y = 2 không song song với trục hoành
Đường thẳng (d’): 2y = 4 hay y = 2 song song với trục hoành
⇒ (d) cắt (d’)
⇒ Hệ phương trình có nghiệm duy nhất.
Vẽ (d1): x + 3y = 2
- Cho y = 0 ⇒ x = 2 được điểm (2; 0).
- Cho x = 0 ⇒ y = 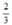 được điểm (0;
được điểm (0; 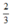 ).
).
Vẽ (d2): y = 2 là đường thẳng đi qua (0; 2) và song song với trục hoành.
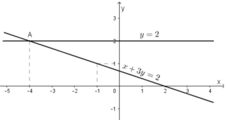
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(-4; 2).
Vậy hệ phương trình có nghiệm (-4; 2).

x = 2 2 x - y = 3
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
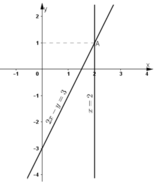
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).

x + 3 y = 2 2 y = 4
Đường thẳng (d): x + 3y = 2 không song song với trục hoành
Đường thẳng (d’): 2y = 4 hay y = 2 song song với trục hoành
⇒ (d) cắt (d’)
⇒ Hệ phương trình có nghiệm duy nhất.
Vẽ (d1): x + 3y = 2
- Cho y = 0 ⇒ x = 2 được điểm (2; 0).
- Cho x = 0 ⇒ y = 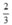 được điểm (0;
được điểm (0; 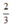 ).
).
Vẽ (d2): y = 2 là đường thẳng đi qua (0; 2) và song song với trục hoành.
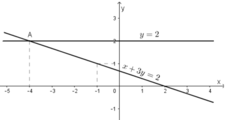
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(-4; 2).
Vậy hệ phương trình có nghiệm (-4; 2).

(I): 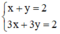
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x + 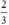 có a’ = -1 ; b’ =
có a’ = -1 ; b’ = 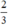
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.

a) (I): 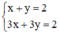
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x + 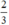 có a’ = -1 ; b’ =
có a’ = -1 ; b’ = 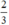
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.
b) (II): 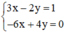
Xét: (d): 3x – 2y = 1 hay (d):
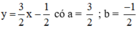
(d’): -6x + 4y = 0 hay (d’):
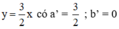
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 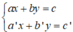
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.

a) \(\hept{\begin{cases}x+y=2\\3x+3y=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3x+3y=6\\3x+3y=2\end{cases}}\)
Dễ thấy điều trên là vô lí nên hệ phương trình không có nghiệm
Xét (II):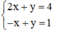
Ta biểu diễn hai đường thẳng (d): 2x + y = 4 và (d’): -x + y = 1 trên mặt phẳng tọa độ.
+ Xét (d): 2x + y = 4 hay (d): y = -2x + 4
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
+ Xét (d’) : -x + y = 1 hay (d’) : y = x + 1.
Chọn x = 0 ⇒ y = 1
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm (0; 1) và (-1; 0).
Nhận thấy (d) và (d’) cắt nhau tại A (1; 2).
Thử lại , thay x =1, y=2 vào các phương trình của hệ (II) ta được:
Vậy hệ phương trình (II) có đúng một nghiệm là (1; 2).