Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải thích: Đáp án B
Phương pháp : Áp dụng công thức của dao động tắt dần của con lắc lò xo
Cách giải :
+ Từ hình vẽ, ta có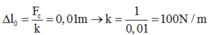 
, với ∆l0 là độ biến dạng của lò xo tại vị trí cân bằng tạm.
Biên độ dao động của vật trong nửa chu kỳ thứ nhất A1, trong nửa chu kì thứ hai, trong nửa chu kì thứ ba và thứ 4 lần lượt là:
A1 = A0 – 1, với A0 là tọa độ ban đầu của vật.
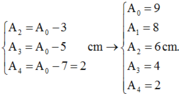
→Tốc độ cực đại của vật trong quá trình dao động 
cm/s.
→Tốc độ trung bình của vật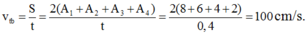 
→Ta có tỉ số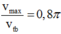 
\(\omega=2\pi f = 9\pi (rad/s)\)
Biên độ \(A=(56-40)/2=8(cm)\)
Gốc thời gian lúc lò xo ngắn nhất --> biên độ (-A) -->\(\varphi=-\pi (rad)\)
Vậy: \(x=8\cos(9\pi t-\pi)(cm)\)
Chọn D.
Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)
Tần số góc: \(\omega=\sqrt{\frac{K}{m}}=10\pi\left(rad\text{/}s\right)\)
Biên độ dao động của vật \(A=\sqrt{x^2+\left(\frac{v}{w}\right)^2}=6\left(cm\right)\)
Lò xo có độ nén cực đại tại biên âm:
\(\Rightarrow\) Góc quét \(=\pi\text{/}3+\pi=\omega t\Rightarrow t=2\text{/}15\left(s\right)\)
chọn B
Tại VTCB : đental = 2.5cm
biên độ : A=(30 - 20)/2 = 5cm
vậy thời gian cần tính là t = T/4 + T/12
0k???
Bài 2 hỏi độ lớn của vật là cái j hả??????
Bai 3. oomega = 20rad/s
tại VTCB denta l = g/omega^2 = 2,5cm
A = 25 - 20 - 2,5 = 2,5cm
li độ tại vị trí lò xo có chiều dài 24cm x=24-22,5 = 1,5cm
Áp dụng CT độc lập với thời gian ta tính được v = 40cm/s
từ đó suy ra động năng thui
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
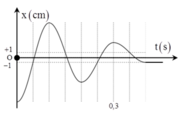
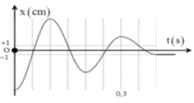
Hướng dẫn
+ Từ hình vẽ, ta có Δ l 0 = F C k = 0 , 01 m → k = 1 0 , 01 = 100 N / m với Δ l 0 là độ biến dạng của lò xo tại vị trí cân bằng tạm.
→ Biên độ dao động của vật trong nửa chu kì thứ nhất A 1 , trong nửa chu kì thứ hai, trong nửa chu kì thứ ba và thứ 4 lần lượt là.
A 1 = A 0 − 1
với A 0 là tọa độ ban đầu của vật
A 2 = A 0 − 3 A 3 = A 0 − 5 A 4 = A 0 − 7 = 2 → A 0 = 9 A 1 = 8 A 2 = 6 A 3 = 4 A 4 = 2
→ Tốc độ cực đại của vật trong quá trình da động v m a x = ω A 1 = 80 π c m / s .
→ Tốc độ trung bình của vật v t b = S t = 2 A 1 + A 2 + A 3 + A 4 t = 2 8 + 6 + 4 + 2 0 , 4 = 100 c m / s
→ Ta có tỉ số v m a x v t b = 0 , 8 π
Đáp án B