Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cường độ dòng điện chạy qua mỗi dây dẫn đều ..........tỉ lệ thuận......... với hiệu điện thế đặt vào hai đầu dây dẫn đó, nhưng hệ số tỉ lệ k có giá trị ...............như nhau...............
- Hãy cho biết : Đồ thị biểu diễn mối quan hệ giữa I và U đối với mỗi đoạn dây dẫn là một đường thẳng có đi qua gốc tọa độ (U = 0, I = 0), vì cường độ dòng điện tỉ lệ thuận với HĐT

\(0,5mm^2=0,5.10^{-6}m^2=5.10^{-7}m^2\)
\(3mm^2=3.10^{-6}m^2\)
Điện trở dây có tiết diện \(0,5mm^2\) là \(R=\rho\frac{l}{s}=\rho\frac{l}{5.10^{-7}}=\frac{U}{R}=\frac{6}{1,5}=4\Omega\Rightarrow\rho l=4.5.10^{-7}=2.10^{-6}\)
Điện trở dây có tiết diện \(3mm^2\) là \(R=\rho\frac{l}{3.10^{-6}}=\frac{2.10^{-6}}{3.10^{-6}}=\frac{2}{3}\Omega\)
Cường độ dòng điện khi đó là
\(I=\frac{U}{R}=6.\frac{3}{2}=9A\)

Gọi HĐT ban đầu là x, CĐDĐ ban đầu là y.
Ta có : U2= x+2,5 ; I2= y+0,2
y+0,2= \(\frac{2,5+x}{R}\)
-=> y+0,2=\(\frac{2,5}{R}\) +\(\frac{x}{R}\)
mà \(\frac{x}{R}\)=y
=> 0,2=\(\frac{2,5}{R}\)
=> R=12,5
Gọi a là CDDD tăng thêm hay giảm đi
Ta có : U3=x-2 ; I3= y+a
y+a=\(\frac{x-2}{R}\)
=> y+a=\(\frac{x}{R}\)-\(\frac{2}{R}\)
=> a=-\(\frac{2}{R}\)=-\(\frac{2}{12,5}\)=-0,16
Vậy cddd giảm đi 0,16 A

1/ Điện trở của một dây dẫn không phụ thuộc vào khối lượng của dây dẫn.
2/ Hiệu điện thế đặt vào điện trở \(R_2\) là: \(U_2=I_2.R_2=2.6=12V\)
Mà \(R_1\) mắc song song với \(R_2\) nên \(U_{tm}=U_1=U_2\)
\(\rightarrow U_1=U_2=12V\)
Áp dụng định luật \(\Omega\): \(I_1=\frac{U_1}{R_1}=\frac{12}{4}=3A\)
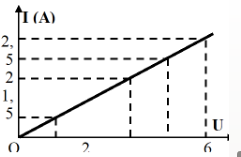
Ta có: Cường độ dòng điện và hiệu điện thế liên hệ với nhau qua biểu thức: I = U R
R là hằng số => đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện vào hiệu điện thế giữa hai đầu dây dẫn có dạng giống đồ thị hàm số y = ax là một đường thẳng đi qua gốc tọa độ.
Đáp án: A