Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
- Sự tăng thể tích của vật rắn khi nhiệt độ tăng gọi là sự nở khối.
+ Công thức độ nở khối:
∆V = V–V0 = βV0∆t
+ Công thức tính thể tích tại t oC:
V = Vo(1 + β∆t). Với V0 là thể tích ban đầu tại t0
Nếu t0 = 0 oC thì V = V0.(1 + βt)

+ Gọi V0 là thể tích của khối lập phương ở 0oC:
V0 = l03
+ V là thể tích của khối lập phương ở t0C:
V = l3 = [l0(1+ α∆t)]3 = l03 (1+α∆t)3
Mà (1+ α∆t)3 = 1 + 3α∆t + 3α2∆t2 + α3∆t3
Vì α khá nhỏ nên α2, α3 có thể bỏ qua.
=> V = l3 = l03 (1+ 3α∆t) = Vo (1+ β∆t) với β = 3α.

Ở nhiệt độ t0 (ºC) cạnh hình lập phương là l0
→ thể tích khối lập phương là:
Ở nhiệt độ t (ºC) cạnh hình lập phương là l
→ thể tích khối lập phương là: V = l3
Mặt khác ta có: l = l0.(1 + αΔt) ⇒ V = l03.(1 + αΔt)3
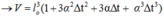
Do α rất nhỏ nên α2 và α3 cũng rất nhỏ, ta có thể bỏ qua.
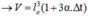
→ ΔV = V – V0 = V0.β.Δt

Ta co: \(a=\frac{V-V_o}{t}\) => \(2a=\frac{2\left(V-V_o\right)}{t}\)
mà \(S=V_ot+\frac{1}{2}at^2\)
\(\Rightarrow2aS=\left(V_ot+\frac{1}{2}at^2\right).\frac{2\left(V-V_o\right)}{t}\)
\(=\frac{V_ot.2\left(V-V_o\right)}{t}+\frac{1}{2}at^2.\frac{2\left(V-V_o\right)}{t}\)
\(=2V_o\left(V-V_o\right)+at\left(V-V_o\right)\)
\(=\left(V-V_o\right)\left(2V_o+at\right)\)
\(=\left(V-V_o\right)\left(V_o+V_o+at\right)\)
\(=\left(V-V_o\right)\left(V_o+V\right)\) ( vì \(V=V_o+at\))
\(=V^2-V^2_o\)
=> \(2aS=V^2-V^2_o\)
\(\Rightarrow S=\frac{V^2-V^2_o}{2a}\)

A. v + v0 = √2aS
B. v2 + v02 = 2aS
C. v - v0 = √2aS
D. v2 - v02 = 2aS
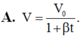
Chọn A
Sự tăng thể tích của vật rắn khi nhiệt độ tăng gọi là sự nở khối.
Công thức độ nở khối: ∆ V = V - V 0 = β V 0 ∆ t
+ Độ nở dài của vật rắn tỉ lệ thuận với độ tăng nhiệt độ Δt và độ dài ban đầu l 0 của vật đó:
∆ l = l - l 0 = a l 0 ∆ t