Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Khi tăng điện dung nên 2,5 lần thì dung kháng giảm 2,5 lần. Cường độ dòng trễ pha hơn hiệu điện thế \(\pi\text{/}4\) nên
\(Z_L-\frac{Z_C}{2,5}=R\)
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì
\(Z_LZ_C=R^2+Z^2_L\)
\(Z_LZ_C=\left(Z_L-\frac{Z_C}{2,5}\right)^2+Z^2_L\)
Giải phương trình bậc 2 ta được
\(Z_C=\frac{5}{4}Z_L\) hoặc \(Z_C=10Z_L\) (loại vì Zl-Zc/2.5=R<0)
\(R=\frac{Z_L}{2}\)
Vẽ giản đồ vecto ta được \(U\) vuông góc với \(U_{RL}\) còn \(U_C\) ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi \(U_L\) và \(U_{LR}\)
\(\tan\alpha=\frac{R}{Z_L}=0,5\)
\(\sin\alpha=1\text{/}\sqrt{5}\)
\(U=U_C\sin\alpha=100V\)
\(U_o=U\sqrt{2}=100\sqrt{2}V\)
chọn C

Nhiệt lượng tỏa ra: \(Q=I^2Rt\)
\(\Rightarrow9.10^5=I^2.10.30.60\)
\(\Rightarrow I=5\)
Biên độ dòng điện \(I_0=5\sqrt{2}\)(A)
Bạn Trần Hoàng Sơn có chút nhầm lẫn, ta tìm đc \(I=5\sqrt{2}A\)
\(\Rightarrow I_0=\sqrt{2}I=10A\)
Chọn C.

Từ ĐK đầu bài ta có:
tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:

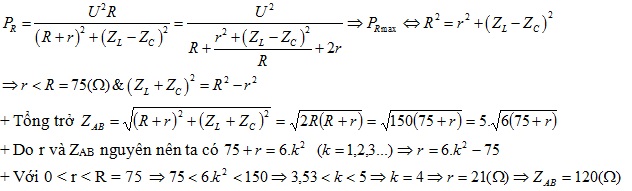
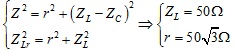
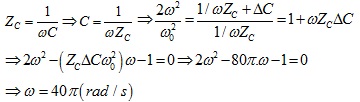
Đáp án D
Ta thấy đồ thị có tính tuần hoàn, cứ cách 1 số ô thì dạng đồ thị lại lặp lại như cũ. Hai đỉnh liên tiếp là 2 hai lần trạng thái lặp lại → khoảng thời gian giữa hai lần đồ thị đạt đến đỉnh là 1 chu kì.
Lại thấy 2 đỉnh cách nhau 3 ô lớn + 3 ô nhỏ = 18 ô nhỏ. Mỗi ô nhỏ tương ứng với 1 mm
→ Khoảng cách giữa hai đỉnh là λ = 18 mm.
Mặt khác băng chuyển động với vận tốc v thì quãng đường băng trượt được sau 1 chu kì T là khoảng cách hai đỉnh λ = vT.
→ T = λ/v = 18/25 = 0,72 s.
Nhịp tim của bệnh nhân này là n = ∆t/T = 60/0,72 = 83,3 nhịp/phút.