Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(\Leftrightarrow\dfrac{7x+10}{x+1}\left(x^2-x-2-2x^2+3x+5\right)=0\)
\(\Leftrightarrow\left(7x+10\right)\left(-x^2+2x+3\right)=0\)
\(\Leftrightarrow\left(7x+10\right)\left(x^2-2x-3\right)=0\)
=>(7x+10)(x-3)=0
hay \(x\in\left\{-\dfrac{10}{7};3\right\}\)
d: \(\Leftrightarrow\dfrac{13}{2x^2+7x-6x-21}+\dfrac{1}{2x+7}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\dfrac{13}{\left(2x+7\right)\left(x-3\right)}+\dfrac{1}{\left(2x+7\right)}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow26x+91+x^2-9-12x-14=0\)
\(\Leftrightarrow x^2+14x+68=0\)
hay \(x\in\varnothing\)

a) \(\dfrac{x^2-x}{x+3}-\dfrac{x^2}{x-3}=\dfrac{7x^2-3x}{9-x^2}\)ĐKXĐ : \(x\ne\pm3\)
\(\Leftrightarrow\dfrac{x\left(x-1\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3x-7x^2}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow x^3-4x^2+3x-x^3-3x^2=3x-7x^2\)
\(\Leftrightarrow-7x^2+3x-3x+7x^2=0\)
\(\Leftrightarrow0x=0\)( luôn đúng )
Vậy \(x\in R\left(x\ne\pm3\right)\)
b) \(\dfrac{2x-1}{x^3+1}=\dfrac{2}{x^2-x+1}-\dfrac{1}{x+1}\)ĐKXĐ : \(x\ne-1\)
\(\Leftrightarrow\dfrac{2x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{2\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\Rightarrow2x-1=2x+2-x^2+x-1\)
\(\Leftrightarrow2x+2-x^2+x-1-2x+1=0\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow x^2-2x+x-2=0\)
\(\Leftrightarrow x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(\text{t/m ĐKXĐ}\right)\\x=-1\left(\text{không t/m ĐKXĐ}\right)\end{matrix}\right.\)
Vậy....

a. (x + 2)(x2 – 3x + 5) = (x + 2)x2
⇔ (x + 2)(x2 – 3x + 5) – (x + 2)x2 = 0
⇔ (x + 2)[(x2 – 3x + 5) – x2] = 0
⇔ (x + 2)(\(x^2\) – 3x + 5 – \(x^2\)) = 0
⇔ (x + 2)(5 – 3x) = 0
⇔ x + 2 = 0 hoặc 5 – 3x = 0
x + 2 = 0 ⇔ x = -2
5 – 3x = 0 ⇔ x = \(\dfrac{5}{3}\)
Vậy phương trình có nghiệm x = -2 hoặc x =\(\dfrac{5}{3}\)
c.\(2x^2\) – x = 3 – 6x
⇔ \(2x^2\) – x + 6x – 3 = 0
⇔ (\(2x^2\) + 6x) – (x + 3) = 0
⇔ 2x(x + 3) – (x + 3) = 0
⇔ (2x – 1)(x + 3) = 0
⇔ 2x – 1 = 0 hoặc x + 3 = 0
2x – 1 = 0 ⇔ x = 1/2
x + 3 = 0 ⇔ x = -3
Vậy phương trình có nghiệm x = \(\dfrac{1}{2}\) hoặc x = -3

2: \(\Leftrightarrow\left(x-4\right)\left(x+1\right)+\left(x+4\right)\left(x-1\right)=2\left(x-1\right)\left(x+1\right)\)
=>x^2-3x-4+x^2+3x-4=2x^2-2
=>2x^2-8=2x^2-2(loại)
3: \(\Leftrightarrow\left(x^2-x\right)\left(x-3\right)+x^2\left(x+3\right)=-7x^2+3x\)
=>x^3-3x^2-x^2+3x+x^3+3x^2+7x^2-3x=0
=>2x^3+6x^2=0
=>2x^2(x+3)=0
=>x=0(nhận) hoặc x=-3(loại)

Giải các phương trình
\(a,3x-2=2x-3\)
\(\Leftrightarrow3x-2x=-3+2\)
\(\Leftrightarrow x=-1\)
Vậy pt có tập nghiệm S = { - 1 }
\(b,2x+3=5x+9\)
\(\Leftrightarrow2x-5x=9-3\)
\(\Leftrightarrow-3x=6\)
\(\Leftrightarrow x=-2\)
Vậy pt có tập nghiệm S = { - 2 }
\(c,11x+42-2x=100-9x-22\)
\(\Leftrightarrow11x-2x+9x=100-22-42\)
\(\Leftrightarrow18x=36\)
\(\Leftrightarrow x=2\)
Vậy pt có tập nghiệm S = { - 2 }
\(d,2x-\left(3-5x\right)=4\left(x+3\right)\)
\(\Leftrightarrow2x-3+5x=4x+12\)
\(\Leftrightarrow2x+5x-4x=12+3\)
\(\Leftrightarrow3x=15\)
\(\Leftrightarrow x=5\)
Vậy pt có tập nghiệm S = { - 5 }
\(e,\dfrac{3x+2}{2}-\dfrac{3x+1}{6}=\dfrac{5}{3}+2x\)
\(\Leftrightarrow\dfrac{3\left(3x+2\right)}{6}-\dfrac{3x+1}{6}=\dfrac{5.2}{6}+\dfrac{2x.6}{6}\)
\(\Leftrightarrow9x+6-3x-1=10+12x\)
\(\Leftrightarrow9x-3x-12x=10-6+1\)
\(\Leftrightarrow-6x=5\)
\(\Leftrightarrow x=-\dfrac{5}{6}\)
Vậy pt có tập nghiệm S = { - \(\dfrac{5}{6}\) }
f,\(\dfrac{x+4}{5}-x+4=\dfrac{x}{3}-\dfrac{x-2}{2}\)
\(\Leftrightarrow\dfrac{6\left(x+4\right)}{30}-\dfrac{30x}{30}+\dfrac{4.30}{30}=\dfrac{10x}{30}-\dfrac{15\left(x-2\right)}{30}\)
\(\Leftrightarrow6x+24-30x+120=10x-15x+30\)
\(\Leftrightarrow6x-30x-10x+15x=30-24-120\)
\(\Leftrightarrow-19x=-114\)
\(\Leftrightarrow x=6\)
Vậy pt có tập nghiệm S = { - 6 }
\(g,\left(2x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(1;-\dfrac{1}{2}\) }
\(h,\left(x+\dfrac{2}{3}\right)\left(x-\dfrac{1}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{2}{3}=0\\x-\dfrac{1}{2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(-\dfrac{2}{3};\dfrac{1}{2}\) }
\(i,\left(3x-1\right)\left(2x-3\right)\left(2x-3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(2x-3\right)^2\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\2x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{3}{2}\\x=-5\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(\dfrac{1}{3};\dfrac{3}{2};-5\) }
\(k,3x-15=2x\left(x-5\right)\)
\(\Leftrightarrow3x-15=2x^2-10x\)
\(\Leftrightarrow-2x^2+3x+10x=15\)
\(\Leftrightarrow-2x^2+13x-15=0\)
\(\Leftrightarrow-2x^2+10x+3x-15=0\)
\(\Leftrightarrow\left(x-5\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\3-2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(5;\dfrac{3}{2}\) }
\(m,\left|x-2\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { -1; 5 }
\(n,\left|x+1\right|=\left|2x+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=2x+3\\x+1=-2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(-2;-\dfrac{4}{3}\) }
\(j,\dfrac{7x-3}{x-1}=\dfrac{2}{3}\) ĐKXĐ : x≠ 1
\(\Leftrightarrow3\left(7x-3\right)=2\left(x-1\right)\)
\(\Leftrightarrow21x-9=2x-2\)
\(\Leftrightarrow x=\dfrac{7}{19}\) ( t/m )
Vậy pt có tập nghiệm S = { \(\dfrac{7}{19}\) }
đ, ĐKXĐ : x ≠ - 1
\(\dfrac{2\left(3-7x\right)}{1+x}=\dfrac{1}{2}\)
\(\Leftrightarrow4\left(3-7x\right)=1+x\)
\(\Leftrightarrow12-28x=1+x\)
\(\Leftrightarrow-29x=-11\)
\(\Leftrightarrow x=\dfrac{11}{29}\) ( t/m)
Vậy pt có tập nghiệm S = { \(\dfrac{11}{29}\) }
\(y,\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{20}{x^2-25}\) ĐKXĐ : \(\left\{{}\begin{matrix}x\ne5\\x\ne-5\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{\left(x+5\right)^2-\left(x-5\right)^2}{\left(x-5\right)\left(x+5\right)}=\dfrac{20}{\left(x-5\right)\left(x+5\right)}\)
\(\Rightarrow20x=20\)
\(\Leftrightarrow x=1\) ( t/m )
Vậy pt có tập nghiệm S = { 1 }
\(\dfrac{1}{x-1}+\dfrac{2}{x+1}=\dfrac{x}{x^2-1}\) ĐKXĐ : \(\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{x+1+2\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow3x-1=x\)
\(\Leftrightarrow2x=1\Leftrightarrow x=\dfrac{1}{2}\)( t/m)
Vậy pt có tập nghiệm S = { \(\dfrac{1}{2}\) }

\(a,\dfrac{3\left(5x-2\right)}{4}-2=\dfrac{7x}{3}-5\left(x-7\right)\)
\(\Leftrightarrow\dfrac{15x-6-8}{4}=\dfrac{7x-15\left(x-7\right)}{3}\)
\(\Leftrightarrow\dfrac{15x-14}{4}=\dfrac{7x-15x+105}{3}\)
\(\Leftrightarrow\dfrac{45x-42}{12}=\dfrac{-32x+420}{12}\)
\(\Leftrightarrow45x+32x=420+42\)
\(\Leftrightarrow77x=462\)
\(\Leftrightarrow x=6\)
\(b,\dfrac{x+5}{2}+\dfrac{3-2x}{4}=x-\dfrac{7+x}{6}\)
\(\Leftrightarrow\dfrac{2x+10+3-2x}{4}=\dfrac{6x-7-x}{6}\)
\(\Leftrightarrow\dfrac{13}{4}=\dfrac{5x-7}{6}\)
\(\Leftrightarrow2\left(5x-7\right)=3.13\)
\(\Leftrightarrow10x-14=39\)
\(\Leftrightarrow10x=53\)
\(\Leftrightarrow x=5,3\)
\(c,\dfrac{x-3}{11}+\dfrac{x+1}{3}=\dfrac{x+7}{9}-1\)
\(\Leftrightarrow\dfrac{3x-9+11x+11}{33}=\dfrac{x+7-9}{9}\)
\(\Leftrightarrow\dfrac{14x+2}{33}=\dfrac{x-2}{9}\)
\(\Leftrightarrow33\left(x-2\right)=9\left(14x+2\right)\)
\(\Leftrightarrow33x-66=126x+18\)
\(\Leftrightarrow-93x=84\)
\(\Leftrightarrow x=-\dfrac{28}{31}\)
\(d,\dfrac{3x-0,4}{2}+\dfrac{1,5-2x}{3}=\dfrac{x+0,5}{5}\)
\(\Leftrightarrow\dfrac{3\left(3x-0,4\right)+2\left(1,5-2x\right)}{6}=\dfrac{x+0,5}{5}\)
\(\Leftrightarrow\dfrac{9x-1,2+3-4x}{6}=\dfrac{x+0,5}{5}\)
\(\Leftrightarrow\dfrac{5x+1,8}{6}=\dfrac{x+0,5}{5}\)
\(\Leftrightarrow5\left(5x+1,8\right)=6\left(x+0,5\right)\)
\(\Leftrightarrow25x+9=6x+3\)
\(\Leftrightarrow19x=-6\)
\(\Leftrightarrow x=-\dfrac{6}{19}\)
\(\Leftrightarrow77x=378\)
\(\Leftrightarrow x=\dfrac{54}{11}\)

Câu 2:
ĐKXĐ: \(\left[{}\begin{matrix}1-9x^2\ne0\\1+3x\ne0\\1-3x\ne0\end{matrix}\right.\Rightarrow \left[{}\begin{matrix}x\ne\dfrac{-1}{3}\\x\ne\dfrac{1}{3}\end{matrix}\right.\)
\(\dfrac{12}{1-9x^2}=\dfrac{1-3x}{1+3x}-\dfrac{1+3x}{1-3x}\left(1\right)\)
\(\left(1\right):\dfrac{12}{\left(1-3x\right)\left(1+3x\right)}-\dfrac{\left(1-3x\right)\left(1-3x\right)}{\left(1-3x\right)\left(1+3x\right)}+\dfrac{\left(1+3x\right)\left(1+3x\right)}{\left(1-3x\right)\left(1+3x\right)}=0\)
\(\Leftrightarrow 12-\left(1-3x-3x+9x^2\right)+\left(1+3x+3x+9x^2\right)=0\)
\(\Leftrightarrow 12-1+3x+3x-9x^2+1+3x+3x+9x^2=0\)
\(\Leftrightarrow12x+12=0\\ \Leftrightarrow12x=-12\\ \Leftrightarrow x=-1\left(TM\right)\)
Vậy \(S=\left\{-1\right\}\)
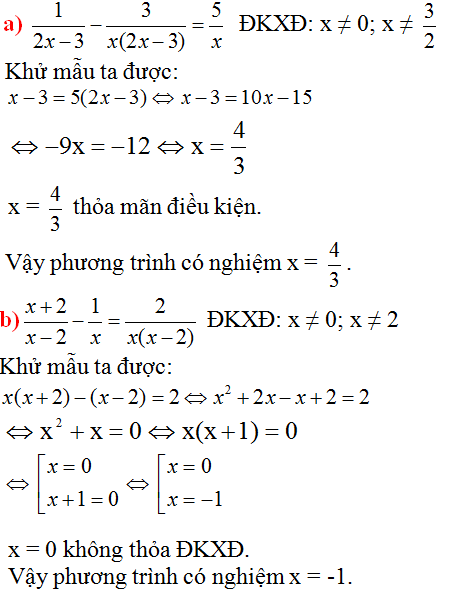




\(\dfrac{x^2-x}{x+3}-\dfrac{x^2}{x-3}=\dfrac{7x^2-3x}{9-x^2}\\ \Leftrightarrow\dfrac{x^2-x}{x+3}-\dfrac{x^2}{x-3}=-\dfrac{7x^2-3x}{\left(x-3\right)\left(x+3\right)}\\ đkxđ:\left\{{}\begin{matrix}x-3\ne0\\x+3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne3\\x\ne-3\end{matrix}\right.\\ \Leftrightarrow\dfrac{\left(x^2-x\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{7x^2-3x}{\left(x-3\right)\left(x+3\right)}=0\\ \Leftrightarrow\dfrac{x^3-3x^2-x^2+3x-x^3-3x^2+7x^2-3x}{\left(x-3\right)\left(x+3\right)}=0\\ \Leftrightarrow\dfrac{0}{\left(x-3\right)\left(x+3\right)}=0\\ \Rightarrow0=0\left(luon.dung\right)\)